Text erkannt:
Flächeninhaltsfunktion (Flächenberechnung mit der Integralrechnung):
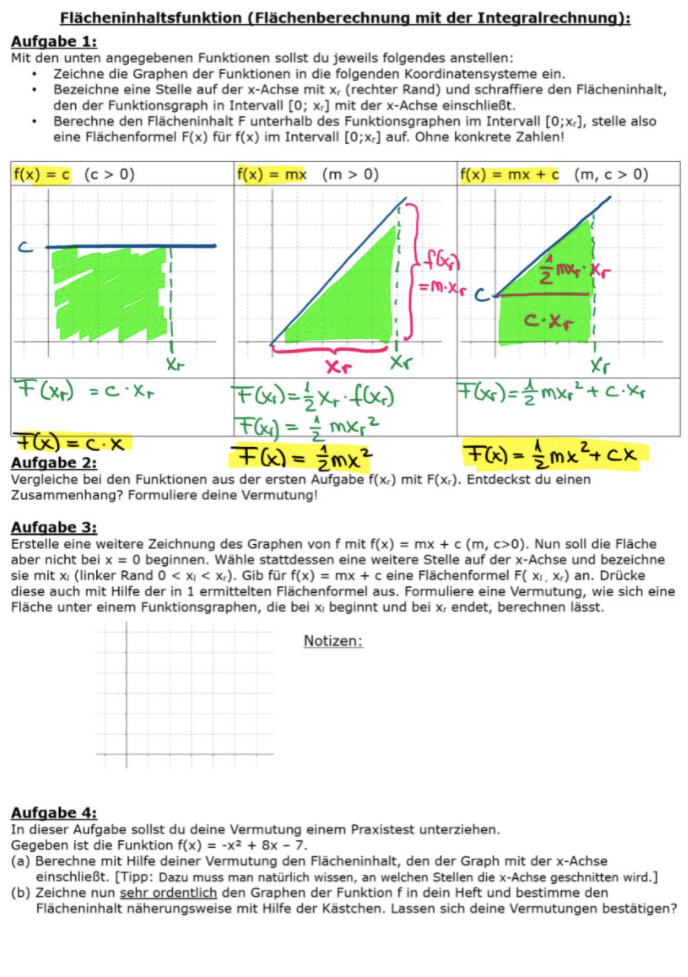
Aufgabe 1:
Mit den unten angegebenen Funktionen sollst du jeweils folgendes anstellen:
- Zeichne die Graphen der Funktionen in die folgenden Koordinatensysteme ein.
- Bezeichne eine Stelle auf der \( x \)-Achse mit \( x_{r} \) (rechter Rand) und schraffiere den Flächeninhalt, den der Funktionsgraph in Intervall \( \left[0 ; x_{r}\right] \) mit der \( x \)-Achse einschlieBt.
- Berechne den Flächeninhalt F unterhalb des Funktionsgraphen im Intervall \( \left[0 ; x_{r}\right] \), stelle also eine Flächenformel \( F(x) \) für \( f(x) \) im Intervall \( \left[0 ; x_{r}\right] \) auf. Ohne konkrete Zahlen!
Vergleiche bei den Funktionen aus der ersten Aufgabe \( f\left(x_{r}\right) \) mit \( F\left(x_{r}\right) \). Entdeckst du einen Zusammenhang? Formuliere deine Vermutung!
Aufqabe 3:
Erstelle eine weitere Zeichnung des Graphen von \( f \) mit \( f(x)=m x+c(m, c>0) \). Nun soll die Fläche aber nicht bei \( x=0 \) beginnen. Wähle stattdessen eine weitere Stelle auf der \( x \)-Achse und bezeichne sie mit \( x_{1} \) (linker Rand \( \left.0<x_{1}<x_{r}\right) \). Gib für \( f(x)=m x+c \) eine Flächenformel \( F\left(x_{1}, x_{r}\right) \) an. Drücke diese auch mit Hilfe der in 1 ermittelten Flächenformel aus. Formuliere eine Vermutung, wie sich eine Fläche unter einem Funktionsgraphen, die bei \( x_{1} \) beginnt und bei \( x_{r} \) endet, berechnen lässt.
Notizen:
Aufgabe 4:
In dieser Aufgabe sollst du deine Vermutung einem Praxistest unterziehen.
Gegeben ist die Funktion \( f(x)=-x^{2}+8 x-7 \)
(a) Berechne mit Hilfe deiner Vermutung den Flächeninhalt, den der Graph mit der x-Achse einschlieBt. [Tipp: Dazu muss man natürlich wissen, an welchen Stellen die \( x \)-Achse geschnitten wird.]
(b) Zeichne nun sehr ordentlich den Graphen der Funktion \( \mathrm{f} \) in dein Heft und bestimme den Flächeninhalt näherungsweise mit Hilfe der Kästchen. Lassen sich deine Vermutungen bestätigen?
Aufgabe:
wie löse ich aufgabe 3 und 4