Hallo,
wie döschwo schon erwähnt hat, gibt es hier mehrere Möglichkeiten. Das Vorgehen, was in der Schule gelehrt wird, sieht wahrscheinlich so aus:
Berechne zunächst einen Vektor \(\vec{n}\), der auf beiden Richtungsvektoren der beiden Geraden senkrecht steht (das hast Du wahrscheinlich sowieso schon gemacht)$$\vec{n} = \begin{pmatrix}3\\ 1\\ -1\end{pmatrix}$$dann bestimmst Du eine Hilfsebene \(E_{g}\), die durch die Gerade \(g\) und durch den Vektor \(\vec{n}\) aufgespannt wird.$$E_{g}:\quad\vec{x} = \begin{pmatrix}2\\ 1\\ 5\end{pmatrix} + r\cdot\begin{pmatrix}1\\ 0\\ 3\end{pmatrix} + t\cdot\begin{pmatrix}3\\ 1\\ -1\end{pmatrix}$$die selbe Ebene \(E_{g}\) in der Koordinatenform:$$E_{g}:\quad -3x+10y+z=9$$Der Schnittpunkt \(H\) der zweiten Geraden \(h\) mit der Ebene \(E_{g}\) ist dann einer der gesuchten Punkte. $$H = h\left(-\frac{6}{11}\right) = \frac{1}{11}\begin{pmatrix}39\\ 20\\ 16\end{pmatrix}$$Wenn Du nun den Fußpunkt \(G\) dieses Punktes auf der Geraden \(g\) berechnest, so hast Du den zweiten Punkt.
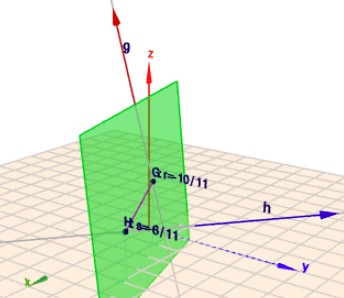
hier siehst Du das ganze nochmal in Geoknecht3D. Klick auf das Bild, dann kannst Du anschließend die Szene mit der Maus rotieren und bekommst so einen besseren räumlichen Eindruck. Die grüne Ebene ist \(E_{g}\).
Falls Du noch Fragen hast, so melde Dich bitte.
Gruß Werner