Wie berechnet man die Momentane Änderungsrate und Ableitungsfunktion? Textaufgabe

Question

Aufgabe:

Früher wurden in den Städten auf Hügeln oder kleineren Bergen Wassertürme gebaut. Durch das in den Türmen gespeicherte Wasser konnte ein ausreichender Wasserdruck für die Versorgung der Wohnungen mit Trinkwasser sichergestellt werden.
Im Folgenden soll die Wassermenge im Speicher eines Wasserturms untersucht werden. Um den nötigen Wasserdruck zu gewahrleisten, soll dafür gesorgt werden, dass ständig mindestens 1000m³ Wasser (Sollwert) im Speicher des Turmes vorhanden sind. Die maximale Füllmenge beträgt 2000m³.  
Für einen bestimmten Tag wird die Wassermenge im Speicher des Turmes im Zeitraum von 6:00Uhr bis 7:30 Uhr für 0 ≤ t ≤ 1,5 durch die Funktion f mit der Gleichung

f(t) = 1000 • t³ - 1000t² - 687 • t + 1467

modelliert. Dabei bezeichnet t die Zeit in Stunden, die seit 6:00 Uhr vergangen ist, und f(t) die Wassermenge im Speicher des Turmes in m³.
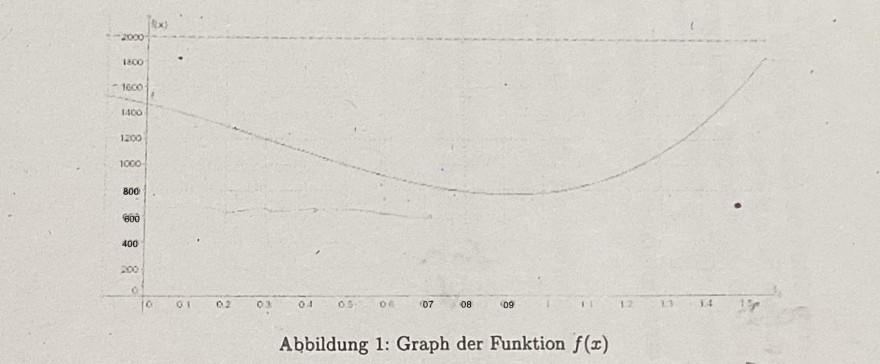
Hier wird der Graph der Funktion, in der folgenden Abbildung dargestellt:

Text erkannt:

Abbildung 1: Graph der Funktion \( f(x) \)

i) Zeige, dass um 7:00 Uhr noch 780m³ Wasser im Speicher des Turms vorhanden sind.
ii) Ermitle näherungsweise die Zeiträume, in denen die Wassermenge über dem Sollwert von 1000m³ liegt.

iii) Berechne f'(1) und interpretiere den Wert im Sachzusammenhang.
iv) Entwickle eine Strategie um den Zeitwert zu bestimmen, bei dem die Wassermenge im Turm minimal ist.

Problem/Ansatz:

Kann einer bitte erklären wie ich bei den Aufgaben i) - iv) berechnen soll?

Danke im Voraus!

Answer 1

Hallo,

i) Setze 1 für t in die Gleichung ein. Das Ergebnis ist 780.

ii) Setze f(t) = 1000 und löse nach t auf.

iii) Setze 1 für t in die 1. Ableitung ein

iv) Setze die 1. Ableitung = 0 und löse nach t auf. Damit berechnest du das Minimum der Funktion, an dem die Steigung = 0 ist.

Gruß, Silvia

Comments

Hallo, danke für deine Antwort, ich hab eine Frage bei Aufgabe ii). Ich hab es so verstanden, dass ich für f(t)  1000 einsetzen soll und dann muss ich = 780 mal t rechnen?

---

Setze f(t) = 1000 und löse nach t auf.

Damit meinte ich

\(1000t^3-1000t^2-687t+1467=1000\)

nach t auflösen.