f(x)= x3-6x2+18+2006
1.Ableitung: f(x)= x2-4x+16
Stimmt nicht
f ´( x ) = 3 * x^2 - 12 * x
Ich nehme einmal an deine 1.Ableitung ist richtig
f ´( x ) = ( x - 2 ) ^2 + 2
Für eine Stelle x die Steigung
z.B. x = 3
f ´( 3 ) = ( 3 - 2 ) ^2 + 2 = 3
Wir wollen aber wissen wann diese Funktion 0, positiv
oder negativ ist. Nicht nur an 1 Stelle.
Jetzt nehmen wir einmal an die
Steigungsfunktion sei
f ´( x ) = ( x - 2 ) ^2 - 3
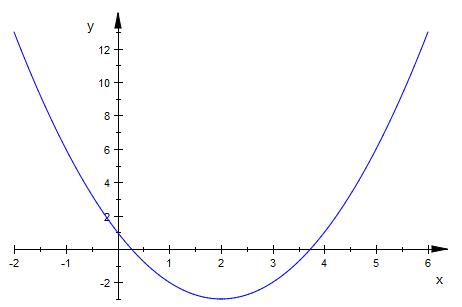
Die Funktionswerte ( y - Achse ) können 0, positiv ( oberhalb )
der x--Achse ) oder negativ sein ( unterhalb der x-Achse.
Alles drei ist möglich.
Ich schrieb
Bei Monotonie-Untersuchung gehe ich wie
folgt vor.
1.Stelle(n) mit waagerechter Tangente bestimmen
f `( x ) = 0
x = ...
2. Monotonie steigend
f ´( x ) > 0
x = ...
3. Monotonie fallend
f ´( x ) < 0
x = ...
Damit hast du für alle Bereiche die Monotonie
ermittelt.
Bitte wende dies Vorgehen einmal an.
Stelle zumindest die Gleichungen und
Ungleichungen einmal auf.