Wände eines Müllcontainers (Winkelfunktionen, Pythagoras)

Question

Aufgabe:

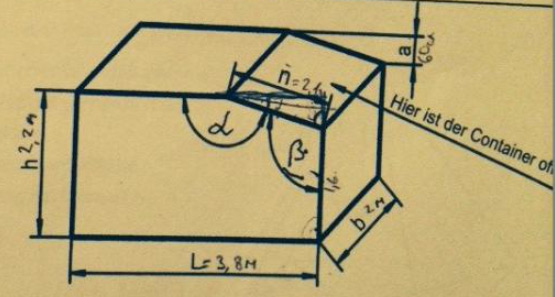
Für die Schlamm-Entsorgung soll ein Mall-Container gebaut werden. Die Länge \( L=3,8 \mathrm{~m} \),
Breite \( b=2 \mathrm{~m} \), Höhe \( h=2,2 \mathrm{~m} \).

Damit man den Schlamm mit einem Bagger einladen kann, muss die Große der Offnung in der Schräge \( n=2,1 \mathrm{~m} \) und in der Höhe von \( \mathbf{a}=60 \mathrm{~cm} \) sein.

a) Für das Zuschneiden der Seitenwände bei der Herstellung braucht man die Große der beiden Winkel \( \alpha \) und \( B \). Berechne die Größe der beiden Winkel! (Tipp: Skizze far das rechtwinklige Dreieck!)

b) Wie viel Liter Schlamm passen maximal in den fertigen Container? Erinnerung: 1 Liter \( =1 \mathrm{dm}^{2} \) (Achtung: Es darf kein Schlamm durch die Öffnung herauslaufen!).

Answer 1

Volumen des Containers  ohne die Höhe der Schräge berechnen, sonst fließt der Schlamm wieder raus.

V = a*b*c oder L *b *H

V = 3,8 *2*(2,2-0,6) =12,16m³

      12,16 m³= 12 160  dm³

      Es passen also  12 100 l Schlamm in den Container.