a) Zeigen Sie anhand einer geeigneten Figur im Einheitskreis und mithilfe des Satzes von Pythagoras, dass die Beziehungen cos(45°) = 1/2 * √2 und sin(45°) = 1/2 * √2 gelten.
Vgl. Link im obigen Kommentar und Skizze hier:
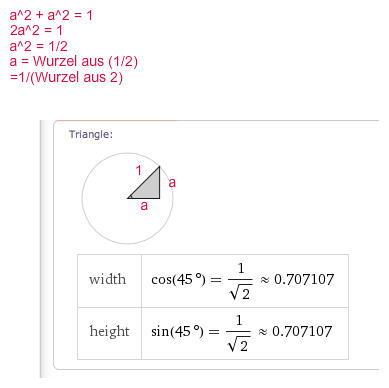
Berechnen Sie hieraus den Wert von tan(45°).
tan(45°) = sin(45°) / cos(45°) = (1/2 * √2) : (1/2 * √2) = 1
b) Zeigen Sie anhand einer geeigneten Figur im Einheitskreis und mithilfe des Satzes von Pythagoras, dass die Beziehungen sin(60°) = √3/2 und cos(60°) = 1/2 gelten. Berechnen Sie hieraus den Wert von tan(60°).
sin und cos: vgl. Link im Kommentar. und Skizze, die ich via https://www.wolframalpha.com/input/?i=cos%2860°%29 erstellt habe.
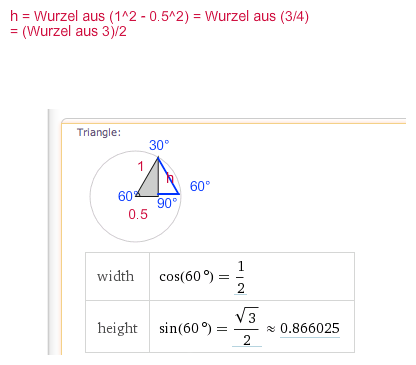
tan(60°) = sin(60°) / cos(60°) = (√3/2) / (1/2) = √3
c) Bestimmen Sie sin(120°) und cos(120°).
Aus Symmetriegründen gilt sin(120°) = sin(60°) = √3/2
und cos(120°) = - cos(60°) = -1/2
Skizze diesmal direkt aus https://www.wolframalpha.com/input/?i=cos%28120°%29
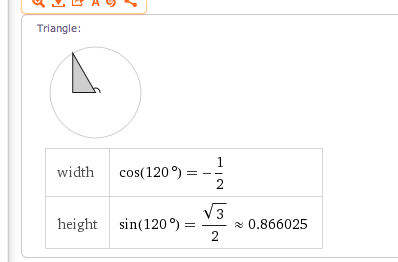
Kontrolliere alle Resultate noch mit dem Taschenrechner.