Aufgabe: Die Vereinfachung des Wurzelterms
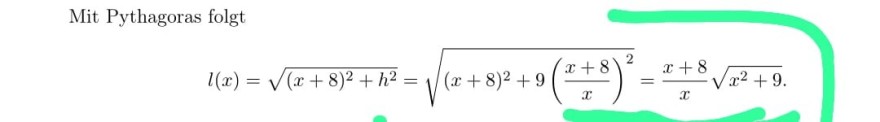
Text erkannt:
Mit Pythagoras folgt
\( l(x)=\sqrt{(x+8)^{2}+h^{2}}=\sqrt{(x+8)^{2}+9\left(\frac{x+8}{x}\right)^{2}}=\frac{x+8}{x} \sqrt{x^{2}+9} . \)
Problem/Ansatz: Den Summenterm muss man ja erstmal faktorisieren. Was sehe ich hier nich?
$$(x+8)^2+9(x+8)^2(x^{-1})^2= (x+8)^2(1+9(x^{-1})^2)$$