Aufgabe:Füllen Sie die Lücken aus
Text erkannt:
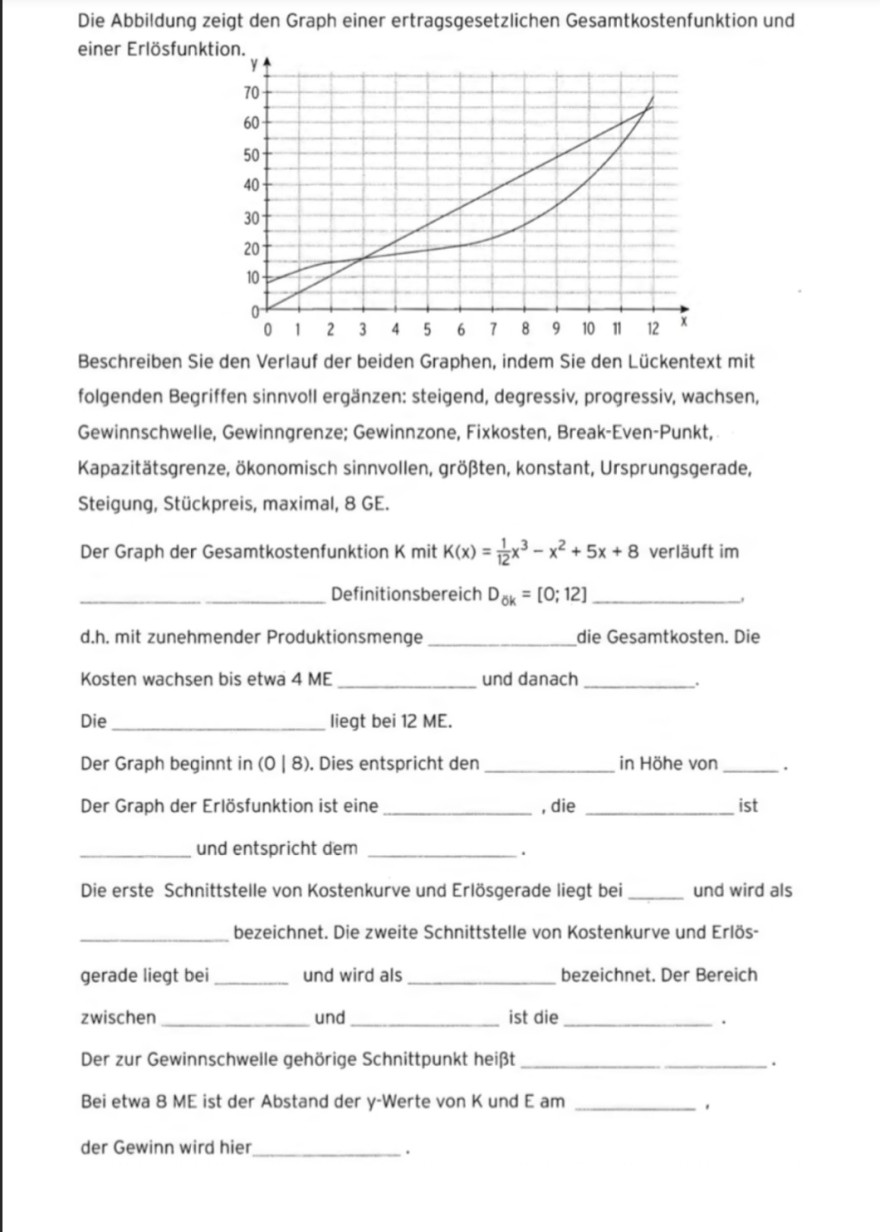
Die Abbildung zeigt den Graph einer ertragsgesetzlichen Gesamtkostenfunktion und einer Erlösfunktion.
Beschreiben Sie den Verlauf der beiden Graphen, indem Sie den Lückentext mit folgenden Begriffen sinnvoll ergänzen: steigend, degressiv, progressiv, wachsen, Gewinnschwelle, Gewinngrenze; Gewinnzone, Fixkosten, Break-Even-Punkt, Kapazitätsgrenze, ökonomisch sinnvollen, größten, konstant, Ursprungsgerade, Steigung, Stückpreis, maximal, 8 GE.
Der Graph der Gesamtkostenfunktion \( K \) mit \( K(x)=\frac{1}{12} x^{3}-x^{2}+5 x+8 \) verläuft im Definitionsbereich \( D_{0 k}=[0 ; 12] \)
d.h. mit zunehmender Produktionsmenge die Gesamtkosten. Die Kosten wachsen bis etwa \( 4 \mathrm{ME} \) und danach Die liegt bei \( 12 \mathrm{ME} \).
Der Graph beginnt in ( \( 0 \mid 8 \) ). Dies entspricht den in Höhe von
Der Graph der Erlösfunktion ist eine , die ist und entspricht dem
Die erste Schnittstelle von Kostenkurve und Erlösgerade liegt bei und wird als bezeichnet. Die zweite Schnittstelle von Kostenkurve und Erlösgerade liegt bei und wird als bezeichnet. Der Bereich zwischen und ist die
Der zur Gewinnschwelle gehörige Schnittpunkt heißt
Bei etwa \( 8 \mathrm{ME} \) ist der Abstand der \( \mathrm{y} \)-Werte von \( K \) und \( E \) am der Gewinn wird hier