Berechnen Sie das Rechteck mit dem möglichst größten Flächeninhalt aus ihrer Glasscheibe

Question

Aufgabe:

Extremwertaufgabe am Graphen

Aus einer Scheibe ist ein Rechteck ausgebrochen.

1. Berechnen Sie das Rechteck mit dem möglichst größten Flächeninhalt aus ihrer Glasscheibe

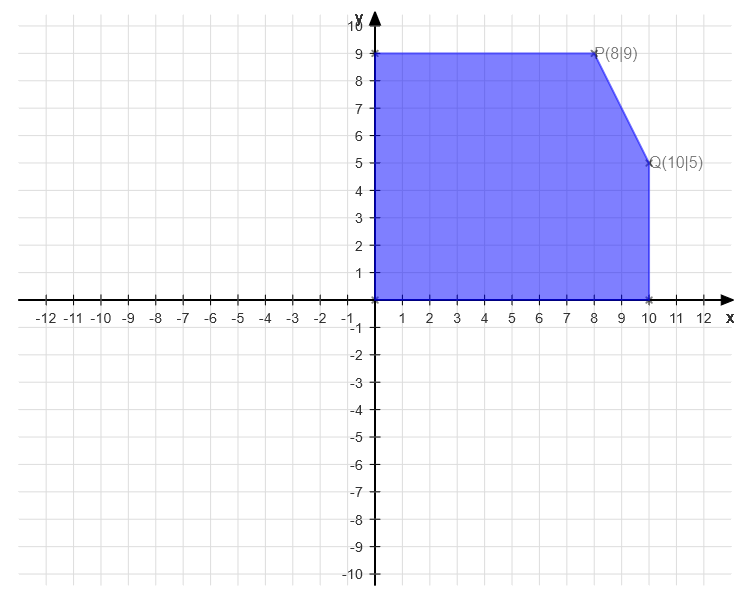
Problem:

Die y-Koordinate (y = 12) liegt ausserhalb der Fläche. Wo liegt der Berechnungsfehler?

Ansatz:

1) Steigung

m = f(x2)-f(x1) / x2-x1 =(9-5)/(8-10) = -2

2) Für die Schräge eine Gleichung aufstellen:

y = m*x+b -> b ist wo x = 0

Punkt Q (10|5) -> x = 10, y = 5 -> y = m*x+b -> 5 = -2*10 +b -> b = 25

y = -2*x +25

3) Formel für den Flächeninhalt:

A = x*y = x(-2*x+25) = -2x²+25x

4) Maximum / erste Ableitung:

A'(x) = -4x + 25 = 0 -> x = 25/4 = 6,25 dm

x = 6,25 in A(x) = -2x²+25 eingesetzt ergibt 78,125 dm²

y = A/x = 78,125/6,25 = 12,5 dm (Außerhalb der Fläche!)

Answer 1

Eine Funktion f (hier eine quadratische Funktion), die auf einem gewissen Intervall [a ... b]  definiert ist, kann Extremwerte nicht nur an Stellen annehmen, an welchen  f'(x) = 0 ist, sondern auch an Randpunkten des Definitionsintervalls. Im vorliegenden Beispiel scheint dies der Fall zu sein. Kümmere dich also mal genau um den Definitionsbereich der Funktion, die du untersuchst !

Answer 2

Dein Ansatz: Bestimme ein Rechteck, bei dem die Koordinatenachsen zum Rand gehören und ein Eckpunkt auf der Schrägen liegt. Daher ist der Defintions Bereich von A eingschränkt: \(A:[8,10] \to \R\).Damit ist A auf diesem Definitionsbereich fallend. Das Max von A wird am linken Rand bei x=8 angenommen.

Answer 3

Deine Rechnung ist wohl richtig, Jetzt fehlt noch die der Definitionsbereich von A und die Erkenntnis, dass es sich um ein Randextremum handeln muss.