Aufgabe:
Abgebildet ist ein Verkehrskreisel, für den die Kreuzungsregel von S. 36 gilt. Die Zahlenangaben stehen für die Durchflussmengen in 100 pro Stunde.
a) Stellen Sie ein lineares Gleichungssystem für x, y, z und t auf und bestimmen Sie die möglichen Lösungen.
b) Welche Mindestgrößen müssen gewählt werden, wenn man die Zu- und Abfahrten berücksichtigt?
c) Welche Maximalgrößen ergeben sich, wenn man berücksichtigt, dass jedes Auto, das in den Kreisel fährt, diesen wieder vor dieser Zufahrt verlässt.
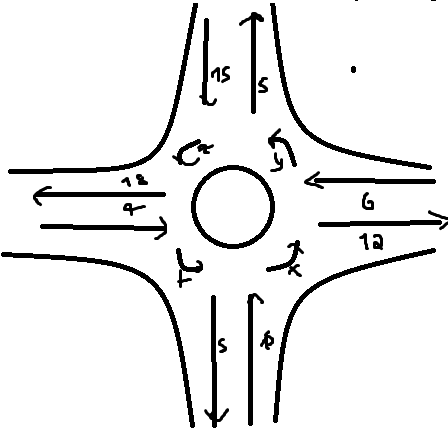
so sieht es in etwa aus( Es tut mir leid, aber ich darf die Buchseite nicht hochladen).
Problem/Ansatz:
Wie berechne ich Maximalkapazitäten von Straßen mit Hilfe von LGS?
Ich soll folgende Aufgabe Lösen. Die Kreuzungsregel auf S. 36 besagt nur, dass in einen Punkt genau so viele Autos rein fahren, wie sie diesen verlassen. Wenn ich mir also z.B. einen Punkt unten Vorstelle, wo 15 in den Kreisverkehr hineinfahren und 5 den Kreisverkehr verlassen. Und außerdem berücksichtige dass nicht jedes Auto bei jeder Ausfahrt den Kreisverkehr verlässt und weiter fahren also auch t Autos rein und x Autos rausfahren, erhalte ich als eine Gleichung folgende:
15 + t = 5 + x
Dies kann man mit jeder Kreuzung machen.
Die Aufgaben a) konnte ich soweit lösen. Bei der b) und c) weiß ich leider nicht, wie ich voran gehen soll. Wie kann ich mathematisch berücksichtigen, dass jedes Auto, das in den Kreisel fährt, diesen wieder vor dieser Zufahrt verlässt ?
Für die a) habe ich folgendes LGS aufgestellt :
x + 6 = y + 12
y+ 15 = 5 + z
z + 4 = 18 + t
t + 15 = 5 + x
und als allgemeine Lösungsmenge, weil das LGS unterbestimmt ist:
L = {(10 + c; 4+ c; 14 + c; c); c e Q}