Aufgabe:
Ein Kinder-Spielturm aus Holz, der aus einem
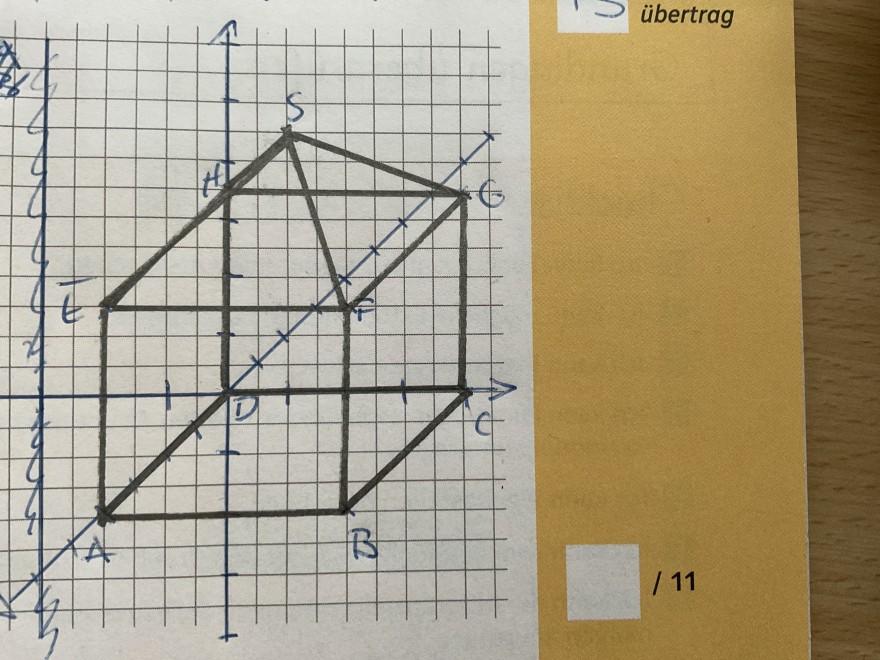
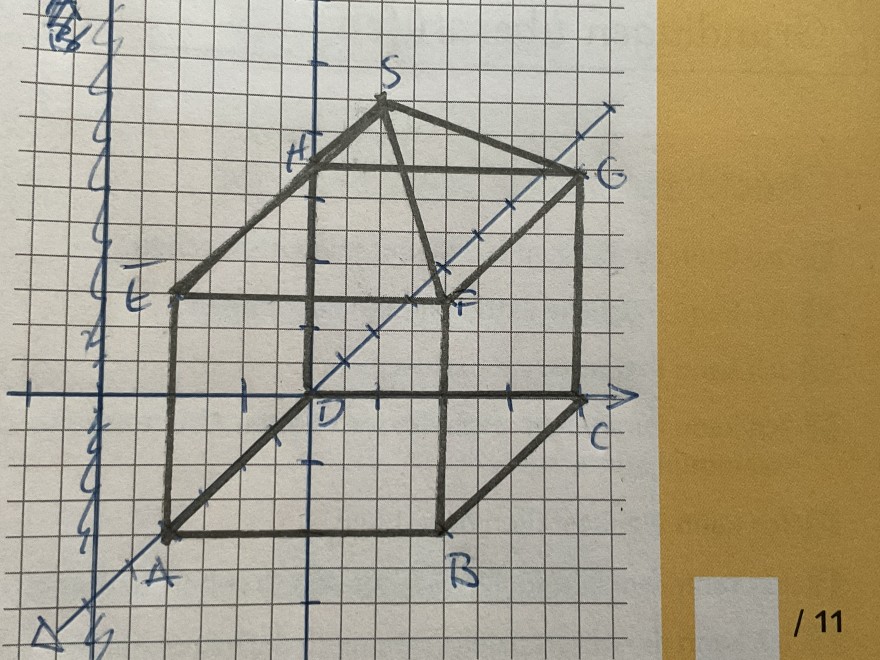
Quader mit aufgesetzter gerader Pyramide besteht, hat eine Gesamthöhe von 5,5 Meter. Bekannt sind die Koordinaten B (4|4|0), D(0/ 0 / 0) und F(4 /4 / 3,5). Die restlichen Punkte sind A (4|0|0), C (0|4|0), E (4| 0 | 3,5),
G(0 l 4 l 3,5). H(0 l 0 l 3,5), S(2 l 2 l 5,5)
Von der Turmspitze S aus sollen vier Kletterseile jeweils so bis zum Boden gespannt werden, dass der Dachfirst SE, SF, SG und SH Teil der jeweiligen Geraden ist. Berechnen Sie die insgesamt benötigte Seillänge.
Berücksichtigen Sie dabei, dass man für die Montage rund 8% Seilmaterial zusätzlich benötigt.
Problem/Ansatz:
Ich habe nun also die Strecken, SE, SF, SG, SH berechnet, um anschließend noch die Höhe des Grund Quaders mit einzuberechnen. Diese Strecke habe ich dann mal vier genommen und mal 1,08.
Die Lösungen gehen jedoch vor, in dem sie geraden mit dem Stützvektor S bilden und diese nach dem Parameter auflösen. Trotzdem bekommen wir unterschiedliche Lösungen raus welche davon ist richtig und wieso ist meine falsch?