Aufgabe:
Aufgabe 2) Die Population von Wildgänsen in einem Naturschutzgebiet verändert sich in einem Zeitraum von 12 Jahren modellhaft beschrieben durch die Funktion f mitf(x) = 0,1x3-8x2 + 8x + 3. (x. Zeit in Jahren, f(x): Anzahl der Wildgänze in
Tausend).
a) Berechne, aus wie vielen
Wildgänsen die Population in diesem Zeitraum
durchschnittlich besteht?
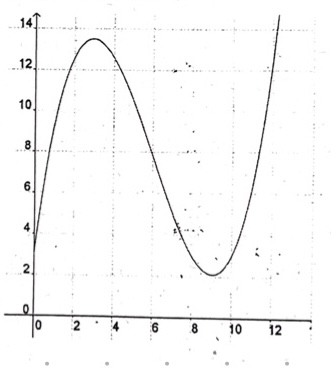
b) Veranschauliche den Mittelwert in Abbildung.
Problem/Ansatz:
Edit: ich hab den Fehler gefunden. Ich habe mit verrechnet. Die richtige Funktion lautet F(x)= 0.1x^4 - 1,8/3x^3+8/2x^2+3x
Daraus folgt das Ergebnis 7,8…
Durch die Formel für den Mittelwert habe ich folgende Gleichung aufgestellt.
1/12*\( \int\limits_{0}^{12} \)(0.1x3-1/8x2+8x+3)dx
= 88.2
Das ergibt ergibt in diesem Zusammenhang anhand des Bildes aber überhaupt keinen Sinn?
Liegt es dann daran das man die Stammfunktion aufstellen muss?
Aufgeleitet, wäre die Funktion ja:
1/12* \( \int\limits_{0}^{12} \)(0.1/4x^4-0.125/3x^3+8/2x^2+3/2x^2)dx
= 349.68
Das passt aber auch nicht? Woher weiß ich denn ob ich aufleiten muss, oder die Funktion benutzen kann?
Danke im Voraus