Steckbriefaufgabe: Punkte A(0/1), B(-1/4), C(2/-5) und D (-2/-15) auf Funktion 3. Grades.

Question

Stimmt das so wie ich unten gemacht habe? Wie soll ich dann mit I weitermachen?

Mit dem II, III, IV weiß ich wie das geht. Soll das Ergebnis von I 0 sein, da es alle 0 ist? 

 

Gesucht ist der Term einer ganzrationalen Funktion3. Grades. Der Graph verläuft durch die Punkte A(0/1), B(-1/4), C(2/-5) und D (-2/-15).

Stellen Sie ein LGS auf und ermitteln sie den Term der Funktion.

I f(0) = 1  
II f(-1) = 4  
III f(2) = -5  
IV f(-2) = -15  

 

I 0*x³ + 0*x² + 0*x² + 0 = 1 
II -1*x³ + (-1)*x² + (-1)*x + (-2) = 4
III 2*x³ + 2*x² + 2*x + 2 = -5  
IV -2*x³ + (-2)*x² + (-2)*x + 2 = -15 

 

I 0*x³ + 0*x² + 0*x + 0 = 1
II -x³ -1x² -1x -1 = 4
III 2x³ + 2x² + 2x + 2 = -5
IV -2x³ -2x² -2x + 2 = -15

Answer 1

 

eine Funktion 3. Grades lautet allgemein

f(x) = ax³ + bx² + cx + d

 

I f(0) = 1  
II f(-1) = 4  
III f(2) = -5  
IV f(-2) = -15

Dies hast Du richtig aufgestellt, aber dann leider die Gleichungen falsch aufgestellt; richtig muss es heißen:

a * 0³ + b * 0² + c * 0 + d = 1 | d = 1

a * (-1)³ + b * (-1)² + c * (-1) + d = 4 | -a + b - c + d = 4

a * 2³ + b * 2² + c * 2 + d = -5 | 8a + 4b + 2c + d = -5

a * (-2)³ + b * (-2)² + c * (-2) + d = -15 | -8a + 4b - 2c + d = -15

Schau mal, ob Du jetzt auf die richtige Lösung kommst :-)

 

Zur Kontrolle:

a = 2,75

b = -2,75

c = -8,5

d = 1

Die Funktion lautet also

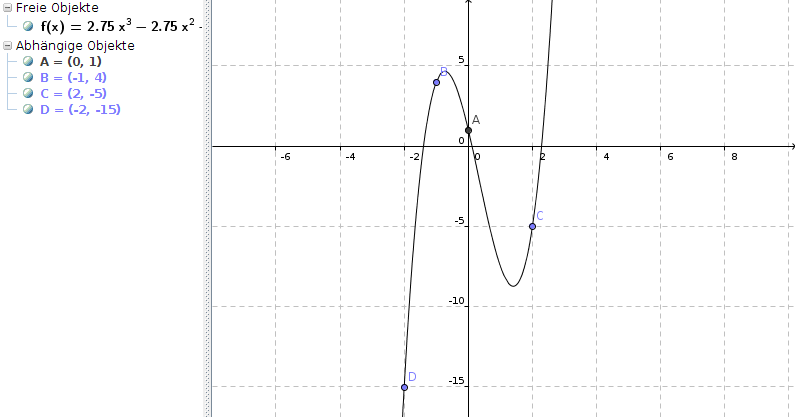
f(x) = 2,75x³ - 2,75x² - 8,5x + 1

Skizze (x- und y-Achse unterschiedliche Maßstäbe!):

 

Besten Gruß

Comments

Danke gerade habe ich auch richtige Lösung von dir geschafft.

Ich hab richtig vertan. Danke nochmal.
Was ich mich eines wundere ist, dass die Lehrerin die Lösung anders geschrieben hat.

Die Lehrerin schrieb die Lösung: f(x) = -x³ + x² + x - 1.

---

Eine Frage habe ich noch. Wie geht mit Polynomdivision weiter? 

(2,75x³ - 2,75x² - 8,5x + 1) : (x ....) = ...

Ich finde in meinem Taschenrechner keinen 0 ..

---

Gern geschehen :-)

 

Wenn der Graph der gesuchten Funktion durch den Punkt A(0|1) geht, dann passt die von Deiner Lehrerin angegebene Lösung bzw. Funktion nicht, wie man durch eine Punktprobe feststellen kann: 

 

f(x) = -x³ + x² + x - 1

f(0) = -0³ + 0² + 0 - 1 = -1 ≠ 1

---

Wozu möchtest Du jetzt eine Polynomdivision machen? Um die Nullstellen zu finden?

---

Ja um die Nullstellen zu finden

---

Eine Polynomdivision ist dann angesagt, wenn Du schon eine Nullstelle hast - ist das hier der Fall?

---

Ich würde die Polynomdivision nur anwenden, wenn ich weder Wurzelziehen noch Ausklammern noch Substituieren kann, da diese Varianten einfach nicht ganz so aufwendig sind wie die Polynomdivision :)

Wollte ich nur kurz erwähnt haben :)

---

Ich sollte die Nullstellen von f berechnen

---

Die Nullstellen sind:

x₁ ≈ 3/25

x₂ ≈ -1,68859

x₃ ≈ 1,84132

Das habe ich auch nur mit einer Mathe-App für mein Handy herausgefunden :-)

Ich würde an Deiner Stelle hier oder in Google einmal nach dem Begriff

"Näherungsverfahren Nullstellenbestimmung"

suchen.

 

Besten Gruß

---

Aber ich darf Newton Verfahren (bzw. Näherungsverfahren) nicht rechnen, weil ich bis jetzt im Unterricht nur Polynomdivision gemacht habe und ich weiß nicht wie ich zu Ende berechnen kann, da ich in der Tabelle keine 0 finde.

---

Schwierig!!

Wenn Du als erste Nullstelle 3/25 geraten hättest - ich weiß nicht, wie man das bewerkstelligen soll - dann müsstest Du folgende Polynomdivision durchführen:

(2,75x³ - 2,75x² - 8,5x + 1) : (x - 3/25) = 2,75x² ...

2,75x³ - 8,25/25 * x²

----------------------------

...

...

 

Das tue ich mir aber jetzt nicht an - bitte habe Verständnis dafür :-D

---

Hmm ok ich könnte auch eigentlich x ausklammern bzw. SvNP oder?

Dann passt es aber auch nicht zu den Ergebnis von
x1 ≈ 3/25

x2 ≈ -1,68859

x3 ≈ 1,84132

---

Ich hab so gerechnet:

 

2,75x³ - 2,75x² - 8,5x + 1 = 0 | x ausklammern

x * (2,75x² - 2,75x - 8,5) = 0 

x₁ = 0

2,75x² - 2,75x - 8,5 = 0 | :2,75

x² - x - 3,09 = 0 | pq Formel

x₁ = - (-1/2) + √(-1/2)² + 3,09 = 2,33

x₂ = - (-1/2) - √(-1/2)² + 3,09 = -1,33

---

Wo ist denn bei Deinem Ausklammern von x die + 1 (letzter Summand linke Seite erste Zeile) geblieben??

---

Ausklammern gehen die 1 doch weg oder? so wie ableitung.

Sonst habe ich keine Ahnung wie das geht.

Vielleicht können Sie mir Schritt zu Schritt zeigen?

Wäre nett von dir ..

---

2,75x³ - 2,75x² - 8,5x + 1 = 0 | x ausklammern

"Ausklammern gehen die 1 doch weg oder? so wie ableitung."

 

Schön wär's :-)

Wenn Du etwas ausklammerst, dann ziehst Du ja einen Faktor vor die Klammer; das heißt, Du musst auch alles innerhalb der Klammer durch den ausgeklammerten Faktor dividieren.

Hier käme also beim Ausklammern folgendes heraus:

x * (2,75x³ / x - 2,75x² / x - 8,5x / x + 1 / x) =

x * (2,75x² - 2,75x - 8,5 + 1/x)

Und das sieht jetzt gar nicht gut aus wegen des letzten Terms innerhalb der Klammer 1/x

:-(

---

Oh jetzt ist echt kompliziert.. Aber danke ..
Ich werd morgen mein Mathelehrerin fragen ..

Vielleicht üben wir dann morgen mit Näherungen ..

Danke trotzdem für die Mühe ..

---

Gern geschehen!

Das wird sich schon klären :-)

Answer 2

Ändere ein paar Vorzeichen in der Aufgabenstellung  [ A=(0|1), B=(-1|4), C=(2|-5), D=(-2|15) ]  und in der Lösung [ f(x)=-x³+x²-x+1 ]  und du erkennst, 1. dass x₀=1 eine Nullstelle und 2. nach Polynomdivision, dass es die einzige Nullstelle ist.