Aufgabe:
Wie entsteht der Graph der Funktion f aus dem Graphen der natürlichen Exponentialfunktion?
Text erkannt:
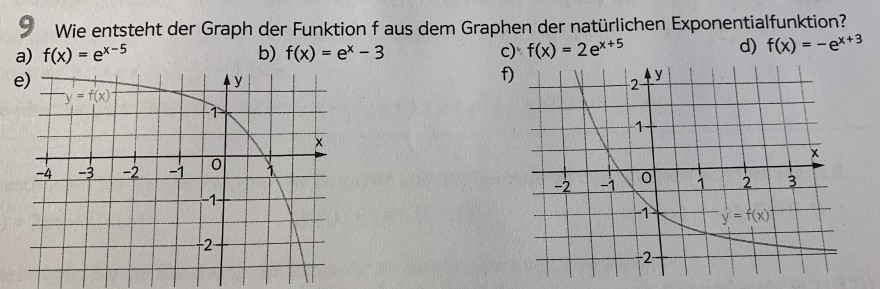
9 Wie entsteht der Graph der Funktion \( f \) aus dem Graphen der natürlichen Exponentialfunktion?
a) \( f(x)=e^{x-5} \)
b) \( f(x)=e^{x}-3 \)
c) \( f(x)=2 e^{x+5} \)
d) \( f(x)=-e^{x+3} \)
f)
Problem/Ansatz:
Ich komme bei dieser Aufgabe nicht weiter, weil ich leider überhaupt keine Ahnung habe, wie ich das lösen soll. Ich würde mich sehr freuen, wenn mir jemand dies vielleicht einmal anhand einer der Funktionen und anhand einer der beiden Graphen erklären könnte, damit ich es nachvollziehen und auf die anderen Aufgaben anwenden kann.