Graphentheorie Aufgabe modellieren

Question

Für sieben Vorlesungen stehen am Semesterende Abschlussklausuren an. Bei der Terminplanung
ist darauf zu achten, dass kein Studierender mehr als eine Klausur pro Tag schreibt.
Ein „+“-Eintrag im Feld (i, j) untenstehender Tabelle bedeutet, dass die Vorlesungen i
und j mindestens einen Studenten gemeinsam haben - die Klausuren für diese Vorlesungen
dürfen also nicht am selben Tag stattfinden.

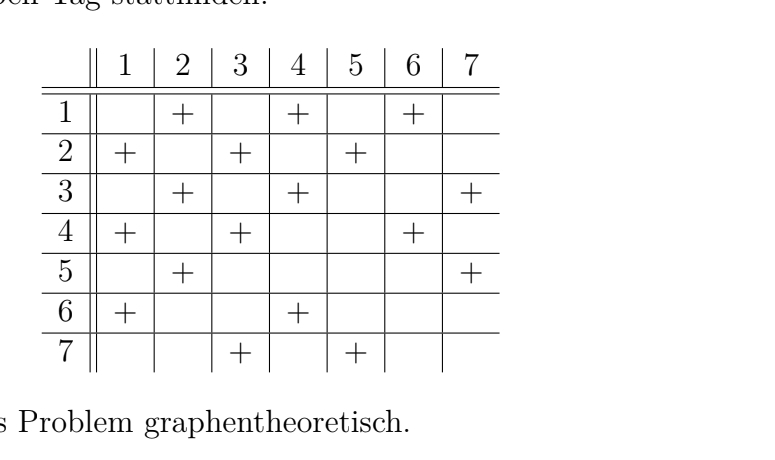
1. Modellieren Sie das Problem graphentheoretisch.

2. Wie viele Tage sind zur Durchführung aller Klausuren mindestens notwendig?
3. Geben Sie einen möglichen Terminplan an.

Kann mir jemand zeigen, wie man diese aufgaben löst danke

Answer 1

1. Modellieren Sie das Problem graphentheoretisch.

Ecken sind die Vorlesungen.

Kanten sind die Beziehung "haben gemeinsame Stundenten".

2. Wie viele Tage sind zur Durchführung aller Klausuren mindestens notwendig?

Finde eine gültige Knotenfärbung mit minimaler Anzahl an Farben.

Comments

Danke

Wäre das so richtig?

Meine Lösung:

2. Der Graph lässt sich nicht mit weniger Farben färben, weil er eine Clique der Größe 3 enthält.Die chromatische Zahl des Graphen ist 3, somit sind mindestens 3 Tage nötig.

3. wäre dann z.B. Am Montag finden die Klausuren der blaugefärbten Knoten, am Dienstag die der rotgefärbten und am Mittwoch die der gelbgefärbten statt.