Hallo zusammen,
ich kann nicht nachvollziehen, weshalb das "c" bei einer partiellen Ableitung nach Pi erhalten bleibt? Alle Variablen außer Pi sollten der Kettenregel nach doch wie eine einfache Zahl behandelt werden? Daraus würde ich schlussfolgern, dass "c" wegfallen müsste. Wo liegt hier mein Denkfehler?
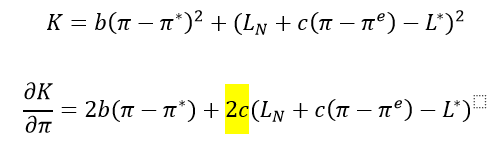
Text erkannt:
\( \begin{aligned} K & =b\left(\pi-\pi^{*}\right)^{2}+\left(L_{N}+c\left(\pi-\pi^{e}\right)-L^{*}\right)^{2} \\ \frac{\partial K}{\partial \pi} & =2 b\left(\pi-\pi^{*}\right)+2 c\left(L_{N}+c\left(\pi-\pi^{e}\right)-L^{*}\right)\end{aligned} \)
Besten Dank vorab und eine schöne Restwoche,
Daniel