Reihe auf Konvergenz untersuchen. Mit dem Wurzelkriterium?

Question

Aufgabe: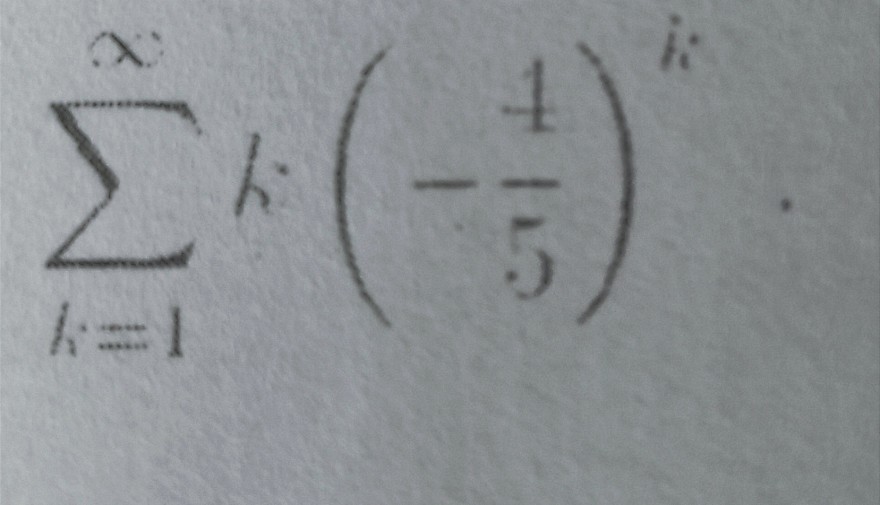

Text erkannt:

\( \sum \limits_{k=1}^{\infty} k\left(-\frac{4}{5}\right)^{k} \)

Problem/Ansatz: ich habe folgende Aufgabe

∑ k *(-4/5)^k

Ich soll die Reihe auf Konvergenz untersuchen. Ich habe dies mit dem Wurzelkriterium geamcht. Die beiden "k" kürzen sich ja mit der k-ten Wurzel. Als Ergebnis hätte ich dann -4/5 heraus.

Meine Frage ist nun ob ich die -4/5 in Betrag schreiben soll ? Dann wäre es ja 4/5

 4/5 ‹ 1→konvergent

Ist es so korrekt ?

Danke

Comments

Hallo,

ich finde die Formulierung "Die beiden "k" kürzen sich ja mit der k-ten Wurzel." bezüglich des "1." k etwas missverständlich. Was Du doch meinst, ist die nichttriviale Aussage

$$\lim_{k \to \infty}\sqrt[k]{k}=1$$

Answer 1

Meine Frage ist nun ob ich die -4/5 in Betrag schreiben soll ? Dann wäre es ja 4/5
4/5 ‹ 1→konvergent
Ist es so korrekt ?

Ja. Im Wurzelkriterium geht es um absolute Konvergenz.