Aufgabe:
Geben Sie zu folgenden Funktionen die jeweilige Umkehrfunktion an. Schränken Sie hierzu den maximal möglichen Definitionsbereich von \( f \) bei Bedarf ein. Skizzieren Sie die Graphen von \( f \) und \( f^{-1} \).
(a) \( f(x)=\sqrt[4]{x} \)
(b) \( f(x)=x^{4} \)
(c) \( f(x)=10^{2 x} \)
(d) \( f(x)=1+\frac{1}{x^{2}} \)
Problem/Ansatz:
Ich versteh die Aufgabe 1 d nicht. Könnte mir jemand auch die Aufgaben a, b, c überprüfen? (Sieht Anhang)
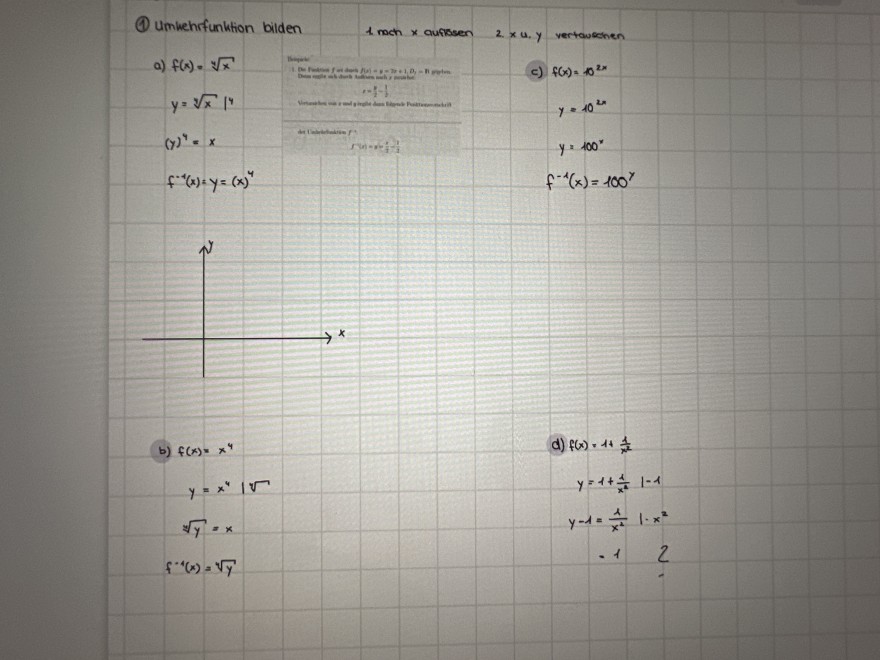
Text erkannt:
(1) Umkehrfunktion bilden 1 moch \( x \) aufirsen \( 2 \times u, y \) vertawechen
b) \( f(x)=x^{4} \)
d) \( f(x)=1+\frac{1}{x^{2}} \)
\( \begin{aligned} y & =x^{4} \mid \sqrt[y]{ } \\ \sqrt[y]{y} & =x \\ f^{-1}(x) & =\sqrt[4]{y} \end{aligned} \)
\( y=1+\frac{1}{x^{2}} \mid-1 \)
\( y-1=\frac{1}{x^{2}} 1 \cdot x^{2} \)
\( -12 \)