Rentenrechnung: Ratenanzahl und Restwert berechnen MIT GEOGEBRA aber ohne Finanzmathematik Befehle

Question

Aufgabe:

Angebot einer Bank zur Rückzahlung eines Kredites von 60.000 €.
Nachschüssige Monatsraten in der Höhe von 300 € bei 2,3 % p.a. Es soll die Ratenanzahl ausgerechnet werden.
Es ist in GeoGebra aber ohne Finanzmathematikbefehle zu lösen und es schreibt mir immer x=? heraus

Ansatz und Problem:

Ich habe mit Ansicht CAS die Eingabe gemacht und dann auf xWelle gedrückt.
Ich kann mir nicht erklären, was da falsch sein sollte.

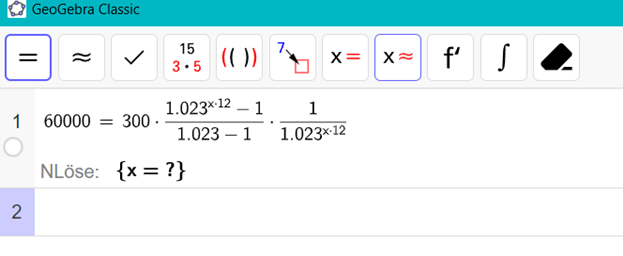
Text erkannt:

GeoGebra Classic
\( 160000=300 \cdot \frac{1.023^{x \cdot 12}-1}{1.023-1} \cdot \frac{1}{1.023^{\times \cdot 12}} \)
NLöse: \( \{x=?\} \)
2

Aufgabe b. dazu

Text erkannt:

GeoGebra Classic
\( \left.=\approx{ }_{3 \cdot 5}^{15}(1)\right)^{7} \sqcup \mathrm{x}=\mathrm{x} \approx \mathrm{f}^{\prime} \int \text { S } \)
\( 160000=300 \cdot \frac{1.023^{x \times 12}-1}{1.023-1} \cdot \frac{1}{1.023 \times 12} \)
NLöse: \( \{\mathrm{x}=?\} \)
2

Davon ausgehend, dass es laut Lösungsteil 251 Raten sind soll die Höhe der Restzahlung wieder mittels GeoGebra und ohne Finanzmathematikbefehle bestimmt werden.

Ansatz und Problem:

Hier war ich sicher die richtige Formel zu wissen aber das Ergebnis ist total unplausibel, was ist da falsch?

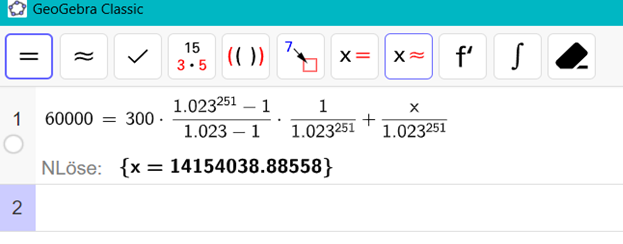
Text erkannt:

GeoGebra Classic
\( 160000=300 \cdot \frac{1.023^{251}-1}{1.023-1} \cdot \frac{1}{1.023^{251}}+\frac{x}{1.023^{251}} \)
NLöse: \( \{x=14154038.88558\} \)
2

Vielen lieben Dank Euch
Martina

Text erkannt:

\( \begin{array}{l} \left.=\checkmark \approx{ }_{3 \cdot 5}^{15}(1)\right)^{7} \succeq x=x=f^{\prime} \int \\ 160000=300 \cdot \frac{1.023^{2}-1}{1.023-1} \cdot \frac{1}{1.023 x} \\ \text { NLöse: }\{x=?\} \end{array} \)
2
\begin{tabular}{c|c|c|c|c|c|c|c|c|}
\( x \) & \( y \) & \( z \) & \( \pi \) & 7 & 8 & 9 & \( \times \) & + \\
\hline \( \mathrm{H}^{2} \) & \( \mathrm{D}^{\prime \prime} \) & \( \sqrt{25} \) & \( e \) & 4 & 5 & 6 & + & - \\
\hline\( < \) & \( > \) & \( \leq \) & \( \geq \) & 1 & 2 & 3 & \( = \) & \( \bigotimes \) \\
\hline( & ) & \( 1 \boxminus \) &, & 0 & & \( < \) & \( > \) & \( \leftarrow \)
\end{tabular}

Comments

Hallo

a) du scheinst mit 2,3% Zinsen pro Monat zu rechnen? x die Anzahl der Jahre nicht der Raten?

bei b) wie kommst du auf die+ x/1,023^251 am Ende deiner Formel  bzw was soll hier x sein?

Answer 1

Es muß heißen

\(60000 = 300 \cdot \frac{\left(1 + \frac{0.023}{12} \right)^{n} - 1}{\frac{0.023}{12}} \cdot \frac{1}{\left(1 + \frac{0.023}{12} \right)^{n}}\)

Folgerichtiger ist mir

\(60000 \; \left(1 + \frac{0.023}{12} \right)^{n} = 300 \cdot \frac{\left(1 + \frac{0.023}{12} \right)^{n} - 1}{\frac{0.023}{12}}\)

Solve($,n); ohne numerisches solve

\( \left\{ n = \frac{2 \; \ln\left(2 \right) + \ln\left(3 \right) - \ln\left(37 \right) + \ln\left(5 \right)}{\ln\left(12023 \right) - 5 \; \ln\left(2 \right) - \ln\left(3 \right) - 3 \; \ln\left(5 \right)} \right\} \)