Hallo,
eine Funktion 3. Grades und ihre 1. Ableitung können dargestellt werden durch
\(f(x)=ax^3+bx^2+cx+d\\ f'(x)=3ax^2+2bx+c\)
Die Flugkurve des Balles hat im Ausgangspunkt einen Tiefpunkt und nach 12 m eine maximale Höhe von 4 m
Ausgangspunkt = Tiefpunkt bedeutet, wenn man den Ausgangspunkt bei x = 0 ansetzt: f'(0) = 0 ⇒ c = 0 und d = 0
Damit bleiben für die Funktion und die 1. Ableitung:
\(f(x)=ax^3+bx^2\\ f'(x)=3ax^2+2bx\)
Aus der maximalen Höhe im Punkt (12|4) kannst du die Gleichungen f(12) = 4 und f'(12) = 0 aufstellen.
Das Gleichungssystem daraus ergibt
\(1728a+144b=4\\432a+24b=0\)
Die Lösungen sind \(a=-\frac{1}{216}\) und \(b=\frac{1}{12}\) und somit lautet der Funktionsterm
\(f(x)=-\frac{1}{216}x^3+\frac{1}{12}x^2\)
Graphisch sieht das so aus:
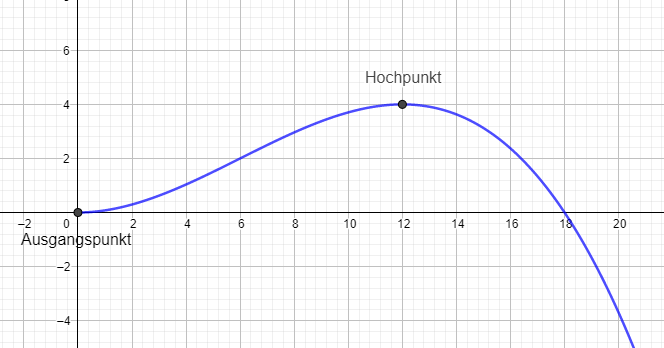
b) Wie hoch darf eine aus Gegenspielern gebildete „Mauer" maximal sein, die in 9,15 m Entfernung vom Ausgangspunkt steht, damit der Ball gerade noch über die Mauer fliegt?
Setze 9,15 für x ein.
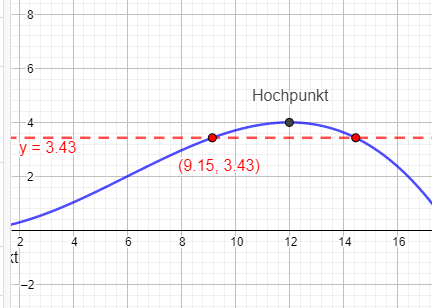
(Die Mauer würde ich gerne sehen).
c) Der Ball senkt sich in einer Höhe von 2 m ins Tor. Bestimmen Sie, wie weit der Freistoß vom Tor entfernt war.
Setze f(x) = 2 und löse nach x auf.
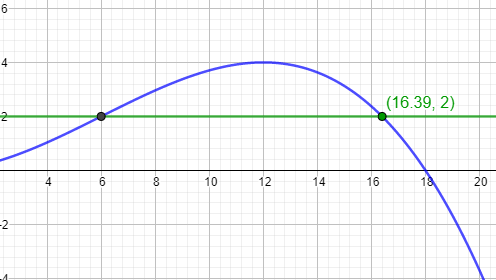
d) Geben Sie an, in welcher Entfernung der Ball am Boden aufgekommen wäre, wenn er nicht ins Tor gegangen wäre.
Berechne die Nullstelle der Funktion.
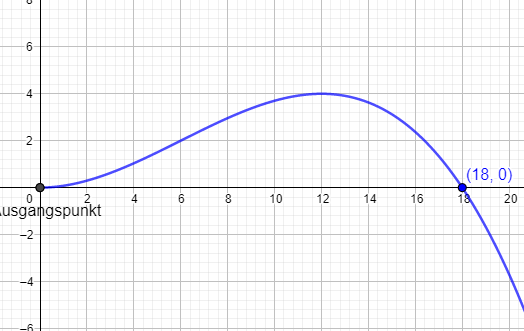
Gruß, Silvia