Lineares Gleichungssystem- unbekannter Paramter und Werte

Question

Aufgabe:

Im Garten des Hauses soll ein Blumenbeet angelegt werden. Dafür sollen Pflanzen dreier Pflan- zengattungen gekauft werden.Eine mögliche Darstellung aller Lösungen des linearen Gleichungssystems lautet:

Um eine mögliche Bepflanzung des Beetes darzustellen, müssen xS, xp und xM nichtnegative ganzzahlige Werte annehmen.

Problem/Ansatz:Untersuchen Sie, welche Werte t unter dieser Bedingung annehmen kann. -> wie gehe ich vor ? ( wie finde ich die einzelnen x Werte ?)

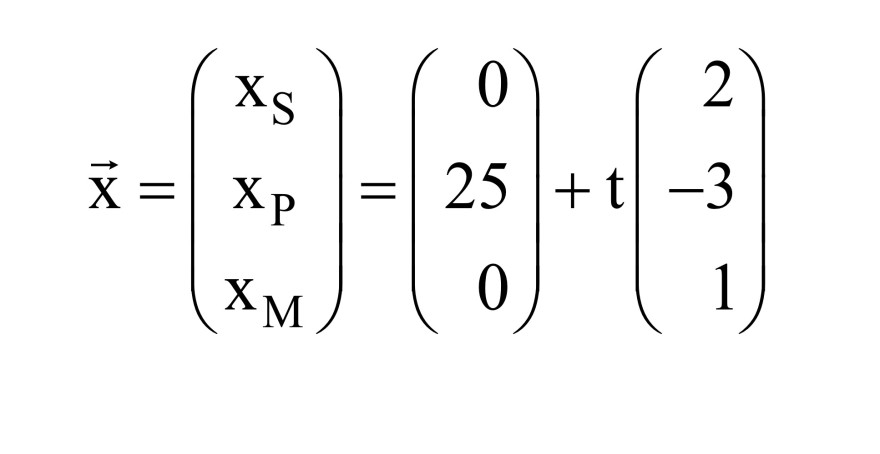
Text erkannt:

\( \vec{x}=\left(\begin{array}{c}x_{S} \\ x_{P} \\ x_{M}\end{array}\right)=\left(\begin{array}{r}0 \\ 25 \\ 0\end{array}\right)+t\left(\begin{array}{r}2 \\ -3 \\ 1\end{array}\right) \)

Answer 1

müssen xS, xp und xM nichtnegative ganzzahlige Werte annehmen.

Formuliere die Nichtnegativität mittels Ungleichungen.

Löse das Ungleichungssystem.

Kümmere dich dann um die Ganzzahligkeit.

Answer 2

xs = 2·t ≥ 0 --> t ≥ 0

xp = 25 - 3·t ≥ 0 --> t ≤ 25/3 = 8.333

xm = t ≥ 0 → t ≥ 0

Damit kann t die Werte 1, 2, 3, ..., 8 annehmen.

Comments

Aber wieso kann ich einfach das xs,xp und xm ignorieren? Bei der Umformung wären die ja eigentlich dabei, oder?

---

Du setzt

xs ≥ 0 und damit 2·t ≥ 0

Da taucht dann kein xs mehr auf. Ich schreibe das nur für die hin die es sonst nicht kapieren, wenn ich es weglasse.