Aufgabe: Hier soll die Stammfunktion bestimmt werden.
Problem/Ansatz: Mir ist nicht klar,wie man hier in den Lösungen den Ausdruck x7 als (x5 - x3 +x)*(1+x2) -x umformen kann ?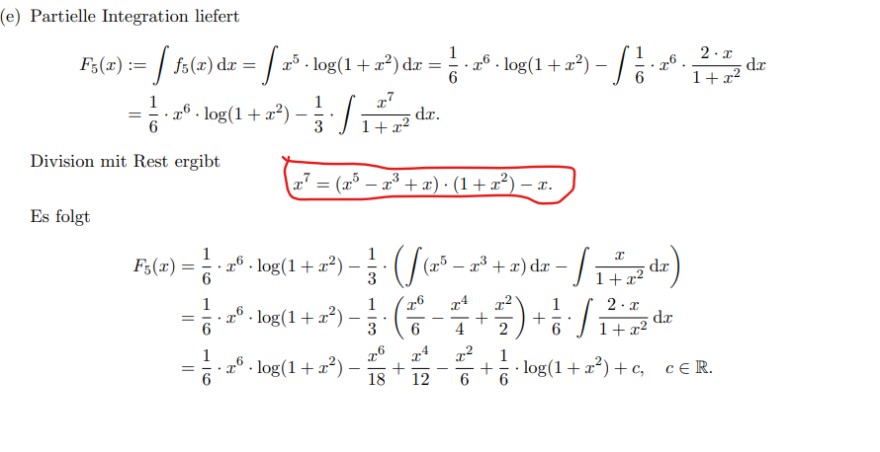
Text erkannt:
(e) Partielle Integration liefert
\( \begin{aligned} F_{5}(x) & :=\int f_{5}(x) \mathrm{d} x=\int x^{5} \cdot \log \left(1+x^{2}\right) \mathrm{d} x=\frac{1}{6} \cdot x^{6} \cdot \log \left(1+x^{2}\right)-\int \frac{1}{6} \cdot x^{6} \cdot \frac{2 \cdot x}{1+x^{2}} \mathrm{~d} x \\ & =\frac{1}{6} \cdot x^{6} \cdot \log \left(1+x^{2}\right)-\frac{1}{3} \cdot \int \frac{x^{7}}{1+x^{2}} \mathrm{~d} x . \end{aligned} \)
Division mit Rest ergibt
\( x^{7}=\left(x^{5}-x^{3}+x\right) \cdot\left(1+x^{2}\right)-x . \)
Es folgt
\( \begin{aligned} F_{5}(x) & =\frac{1}{6} \cdot x^{6} \cdot \log \left(1+x^{2}\right)-\frac{1}{3} \cdot\left(\int\left(x^{5}-x^{3}+x\right) \mathrm{d} x-\int \frac{x}{1+x^{2}} \mathrm{~d} x\right) \\ & =\frac{1}{6} \cdot x^{6} \cdot \log \left(1+x^{2}\right)-\frac{1}{3} \cdot\left(\frac{x^{6}}{6}-\frac{x^{4}}{4}+\frac{x^{2}}{2}\right)+\frac{1}{6} \cdot \int \frac{2 \cdot x}{1+x^{2}} \mathrm{~d} x \\ & =\frac{1}{6} \cdot x^{6} \cdot \log \left(1+x^{2}\right)-\frac{x^{6}}{18}+\frac{x^{4}}{12}-\frac{x^{2}}{6}+\frac{1}{6} \cdot \log \left(1+x^{2}\right)+c, \quad c \in \mathbb{R} . \end{aligned} \)
Text erkannt:
(b) Wegen des 1. Teils lässt sich \( f \) als
\( f(x)=\sqrt{1+\sin (\pi \cdot x)}=\sqrt{2} \cdot\left|\cos \left(\left(x-\frac{1}{2}\right) \cdot \frac{\pi}{2}\right)\right| \)
schreiben. Mit der Potenzreihenentwicklung des Kosinus ergibt sich
\( \sqrt{2} \cdot \cos \left(\left(x-\frac{1}{2}\right) \cdot \frac{\pi}{2}\right)=\sqrt{2} \cdot \sum \limits_{n=0}^{\infty}(-1)^{n} \cdot \frac{\left(x-\frac{1}{2}\right)^{2 n}}{(2 n) !} \cdot\left(\frac{\pi}{2}\right)^{2 n}, \quad x \in \mathbb{R} . \)
Für \( x \in\left(-\frac{1}{2}, \frac{3}{2}\right) \) gilt \( -\frac{\pi}{2}<\left(x-\frac{1}{2}\right) \cdot \frac{\pi}{2}<\frac{\pi}{2} \) und damit
\( \cos \left(\left(x-\frac{1}{2}\right) \cdot \frac{\pi}{2}\right)>0 \)
Für jedes \( x \in\left(-\frac{1}{2}, \frac{3}{2}\right) \) folgt
\( f(x)=\sqrt{1+\sin (\pi \cdot x)}=\sqrt{2} \cdot \cos \left(\left(x-\frac{1}{2}\right) \cdot \frac{\pi}{2}\right)=\sqrt{2} \cdot \sum \limits_{n=0}^{\infty}(-1)^{n} \cdot \frac{\left(x-\frac{1}{2}\right)^{2 n}}{(2 n) !} \cdot\left(\frac{\pi}{2}\right)^{2 n} \)
und die Potenzreihe auf der rechten Seite ist zugleich die Taylorentwicklung von \( f \) im Punkt \( x_{0}=\frac{1}{2} \).