Aquarium Rechenaufgabe: Volumen / Kosten

Question

Aufgabe:

Ein Aquarium soll aus fünf Glasscheiben mit Spezialhaftkleber zusammengeklebt werden. Im nebenstehenden Bild sind die fünf Glasscheiben blau dargestellt.

Dabei gibt es unterschiedliche Kleber: einen Bodenkleber für die Fugen zwischen Boden- und Seitenfläche und einen Seitenkleber für die Fugen zwischen zwei Seitenflächen. Der Seitenkleber kostet 2 Euro pro Meter Fuge, der Bodenkleber kostet 8 Euro pro Meter Fuge. Das Aquarium soll 200 Liter Wasser fassen können. Bestimmen Sie die Breite (x), Tiefe (y) und Höhe (z) des Aquariums so, dass die Gesamtkosten für die Kleber minimal sind.

Breite:

Tiefe:

Höhe:

Gesamtkosten für die Kleber:

Ich komme einfach hier nicht weiter und weiß wirklich nicht wie ich damit anfangen soll.

Answer 1

Hm,

das wäre evtl. ein Ansatz wenn ihr das Verfahren besprochen habt?

6 * 2x + 6 * 2y + 4 * 2z -> min

x y z = 6 / 25

https://www.geogebra.org/m/bMPMqBaT

der Graph muß allerdings nachbearbeitet werden zu

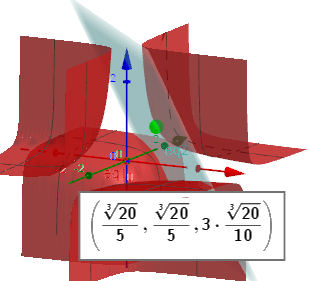
\(KritPkte:= \left(\frac{\sqrt[3]{20}}{5}, \frac{\sqrt[3]{20}}{5}, 3 \cdot \frac{\sqrt[3]{20}}{10}\right) \\ MaxMin \, :=  \, 19.54381\)

Viel kommt dabei aber nicht rum...