Ebene parallel zur Y-Achse

Question

Aufgabe:

Ebene parallel zu Koordinatenachse Verständnis

Problem/Ansatz:

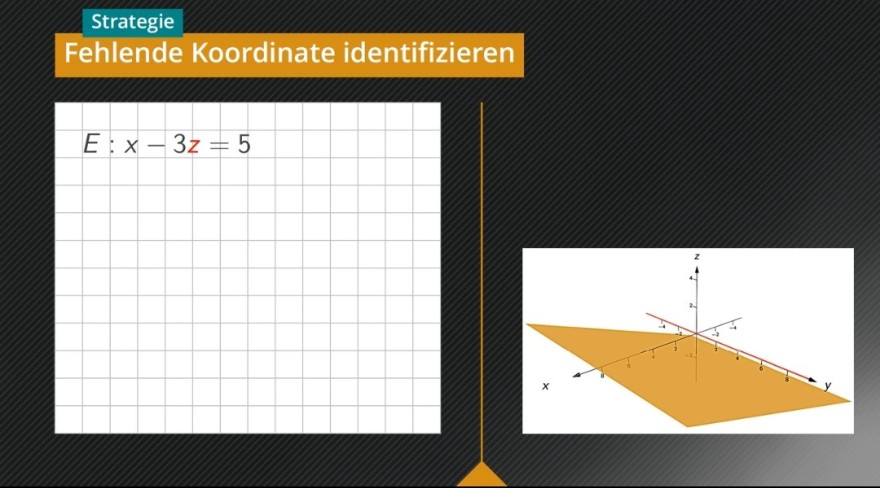
In der Darstellung soll eine zur Y-Achse parallele Ebene dargestellt sein.

Ich kann das jedoch in der Abbildung nicht erkennen. Dass die Ebene die Y-Achse nicht schneidet ist deutlich, aber sie verläuft räumlich gesehen doch über und unter ihr. Wie ist das mit der Parallelität zu verstehen? Vielleicht habe ich mich auch noch nicht wieder an die dreidimensionale Darstellung gewöhnt und übersehe etwas

Comments

Du sagst selber, dass die Ebene die y-Achse nicht schneidet, sondern "über oder unter ihr" verläuft.

Was mehr erwartest du von Parallelität?

---

Naja also bei einer Geraden im Bezug auf eine Koordinatenachse müsste die Gerade doch genau unter oder überhalb der Achse verlaufen und wenn die Gerade die Achse nicht schneidet, aber quer dort drüber oder drunter verläuft wäre sie doch nicht mehr parallel.

Bei einer Ebene wäre doch dann eigentlich nur eine Gerade auf der Ebene parallel zur Achse oder irre ich mich da?

---

Wenn eine Gerade der Ebene parallel zur y-Achse verläuft, also die, die genau darunter ist, können die anderen Geraden sich doch nicht anders verhalten. Sie sind zwar weiter entfernt, haben aber die gleiche Steigung.

---

Verstehe. Danke dir, war ein Denkfehler

---

Zwei Geraden, die parallel verlaufen, haben an jeder Stelle den gleichen Abstand.

Eine Gerade, die parallel zur Ebene verläuft, hat auch an jeder Stelle den gleichen Abstand zur Ebene.

Answer 1

Aloha :)

Wenn du die Koordinatengleichung der Ebene$$x-3z=5\quad\text{bzw.}\quad x=5+3z$$

als Parametergleichung aufschreibst:$$\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}5+3z\\y\\z\end{pmatrix}=\begin{pmatrix}5\\0\\0\end{pmatrix}+y\pink{\begin{pmatrix}0\\1\\0\end{pmatrix}}+z\begin{pmatrix}3\\0\\1\end{pmatrix}$$

erkennst du, dass die Ebene einen Richtungsvektor parallel zur \(y\)-Achse hat.

Comments

Mir geht es darum, wie man das anhand der Abbildung sieht. Ich denke, ich bin noch zu sehr im zweidimensionalen Koordinatensystem mit meiner Denkweise, denn ich verstehe nicht wie die "schiefe" Ebene auf einmal parallel zur Y-Achse sein kann.