Lineare Funktion: i schneidet die y-Achse bei B (0/3) und ist parallel zur Geraden k mit k(x)= -2x-1

Question

Gib de Funktionsgleichung der folgenden Geraden an.
d) i schneidet die y-Achse bei B (0/3) und ist parallel zur Geraden k mit k(x)= -2x-1 .
e) m ist parallel zur x-Achse und geht durch den Punkt S (-4/2).

Answer 1

Diese Aufgabe löst du über die Normalform der linearen Funktion: f(x) = m*x + n = y

d) Bekannt: i ist parallel zu k, d.h. beide haben die gleiche Steigung mit m = -2

I. m einsetzen in:

f(x) = m*x + n = y

f(x) = -2*x + n = y

II. Nun kennen wir den Punkt B(0|3), diesen einsetzen:

f(x) = -2*x + n = y

f(0) = -2*0 + n = 3

-2*0 + n = 3

n = 3

III. Wert für n in f einsetzen:

f(x) = -2*x + 3 = y

Kontrolle per Grafik:

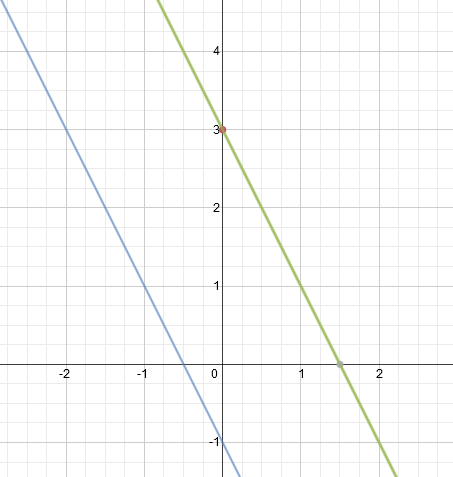
Aufgabe e löst du genauso (parallel zur x-Achse heißt Steigung m=0). Schaffst du das?