Hallo Roland,
Die Parallele zu CW durch B schneidet AC in D, Ist dann DW die Winkelhalbierende des Winkels mit dem Scheitel D im Dreieck ABD?
Nein - ist sie nicht. Wenn man \(\angle ACB = \gamma\) in etwa zu 90° macht und \(\angle BAC=\alpha\) deutlich größer als \(\angle CBA = \beta\), dann ist das offensichtlich nicht der Fall
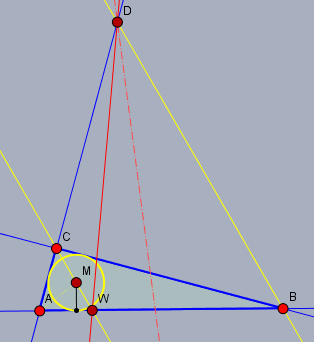
Die interessantere Frage ist:
Welche Eigenschaft hat ein Dreieck \(\triangle ABC\), wenn \(DW\) die Winkelhalbierende zu \(\angle ADB\) ist?
Die Antwort ist: Für das Quadrat der Seite \(|AB|=c\) muss gelten$$c^2 = b^2 +ab-a^2-\frac{a^3}{b} \quad\quad a = |BC|,\space b=|CA|\quad a \lt b$$Für \(b \lt a\) müssen \(a\) und \(b\) vertauscht werden.
Gruß Werner