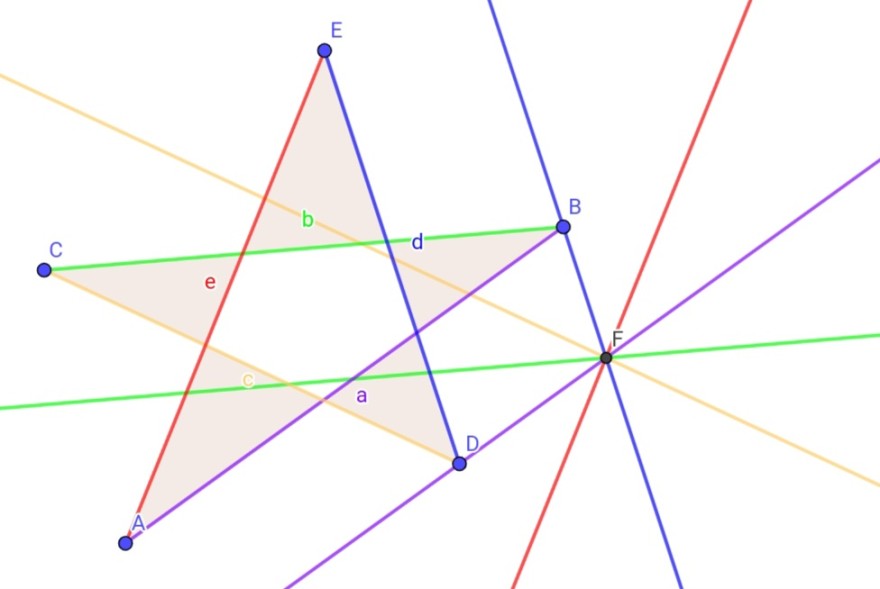
Die Winkel im inneren Fünfeck seien α,β,γ,δ und ε. Ihre Summe beträgt 3•180°=540°.
Die Summe der Innenwinkel der äußeren Dreiecke beträgt s_∆= 5•180°=900°.
Davon subtrahiere ich die Summe s10 der zehn Nebenwinkel der Fünfecks-Winkel.
s10
=2•(180°-α +180°-β +180°-γ +180°-δ +180°-ε)
=2•(5•180°-3•180°)
=720°
s_∆-s10=900°-720°=180°
:-)
PS:
Es kann natürlich auch noch vorkommen, dass eine Zacke innerhalb des Fünfecks liegt...
PPS:
Hier noch eine geometrische Lösung mit Parallelverschiebungen.