Aufgabe:
Berechne die Varianz
Problem/Ansatz:
Text erkannt:
\begin{tabular}{|l|l|l|l|l|}
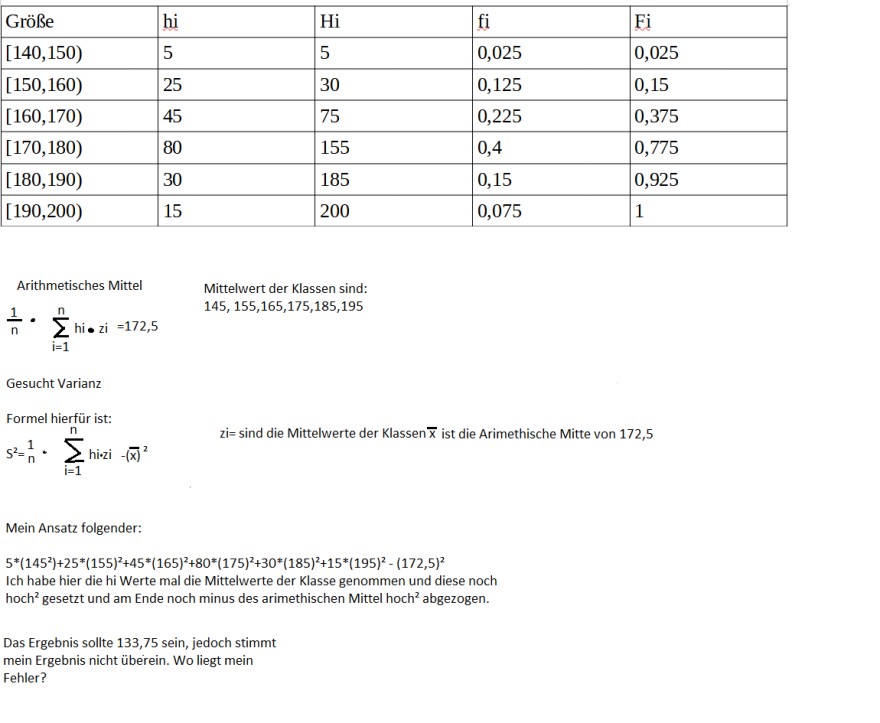
\hline Größe & hi & \( \mathrm{Hi} \) & fi & Fi \\
\hline\( [140,150) \) & 5 & 5 & 0,025 & 0,025 \\
\hline\( [150,160) \) & 25 & 30 & 0,125 & 0,15 \\
\hline\( [160,170) \) & 45 & 75 & 0,225 & 0,375 \\
\hline\( [170,180) \) & 80 & 155 & 0,4 & 0,775 \\
\hline\( [180,190) \) & 30 & 185 & 0,15 & 0,925 \\
\hline\( [190,200) \) & 15 & 200 & 0,075 & 1 \\
\hline
\end{tabular}
Arithmetisches Mittel
Mittelwert der Klassen sind:
\( \frac{1}{n} \cdot \sum \limits_{i=1}^{n} h i \cdot z i=172,5 \)
Gesucht Varianz
Formel hierfür ist:
\( S^{2}=\frac{1}{n} \cdot \sum \limits_{i=1}^{n} \) hi.zi \( -(\bar{x})^{2} \)
\( z \mathrm{zi}= \) sind die Mittelwerte der Klassen \( \overline{\mathrm{x}} \) ist die Arimethische Mitte von 172,5
Mein Ansatz folgender:
\( 5^{*}\left(145^{2}\right)+25^{*}(155)^{2}+45^{*}(165)^{2}+80^{*}(175)^{2}+30^{*}(185)^{2}+15^{*}(195)^{2}-(172,5)^{2} \)
Ich habe hier die hi Werte mal die Mittelwerte der Klasse genommen und diese noch hoch \( { }^{2} \) gesetzt und am Ende noch minus des arimethischen Mittel hoch \( { }^{2} \) abgezogen.
Das Ergebnis sollte 133,75 sein, jedoch stimmt mein Ergebnis nicht überein. Wo liegt mein
Fehler?
Ich befolge die Formel, setze alles ein, jedoch komme ich nicht auf das richtige Ergebnis von 133,75. Wo liegt mein Fehler?