Aloha :)
Das Newton-Verfahren zur Nullstellenberechung einer Funktion \(f(x)\) lauft so...
1) Wähle einen Schätzwert \(x_0\) für die Nullstelle.
2) Berechne die Tangente \(t(x)\) an die Funktion \(f(x)\) am Schätzwert \(x_0\):$$t(x)=f(x_0)+f'(x_0)\cdot(x-x_0)$$
3) Berechne den Schnittpunkt dieser Tangente mit der \(x\)-Achse.$$0\stackrel!=t(x)\implies x=-\frac{f(x_0)}{f'(x_0)}+x_0$$
4) Wahle diesen Schnittpunt als neuen Schätzwert \(x_1\) und gehe zu Schritt 2).
Formal berechnest du also die Folge:$$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\quad;\quad x_0=\text{gewählter Schätzwert}$$
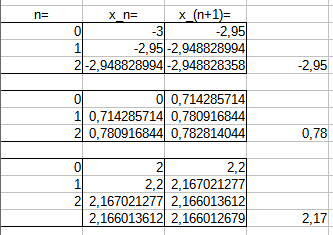
Für die Funktion in der Aufgabenstellung ist$$f(x)=x^3-7x+5\quad;\quad f'(x)=3x^2-7$$und die Newton-Folge ist demnach:$$x_{n+1}=x_n-\frac{x_n^3-7x_n+5}{3x_n^2-7}$$
Das liefert folgende Nullstellen: