Ich mach es mal mit der Brechstange: Inklusion-Exklusion-Prinzip.
Jede injektive Abbildung (ab jetzt kurz iA) entspricht genau einer Permutation einer Auswahl von 5 Zahlen aus \(\{1,2,3,4,5,6\}\). Wenn \(I\) die Menge aller iA ohne jegliche Nebenbedingung bezeichnet, haben wir also
\(|I| = \binom 65\cdot 5! = 6!\)
Es ist nun (für mich) einfacher, zunächst die Anzahl der iA zu bestimmen, die jeweils eine der entgegengesetzten Bedingungen erfüllen. Zum Beispiel:
\(I_a\) - Menge der iA mit \(f(a) {\color{blue}{=}}2 \) oder \(f(a) {\color{blue}{=}} 3\). So erhalten wir
\(|I_a| = 2\cdot 5\cdot 4\cdot 3\cdot 2= 2\cdot 5!\)
Analog definierst du \(I_b,I_c,I_d\) und erhältst (bitte selber nachechnen)
\(|I_b| = 2\cdot 5!,\;|I_c| = 1\cdot 5!,\; |I_d| = 3\cdot 5!\)
Um die Formel des Inklusion-Exklusion-Prinzips anwenden zu können, musst du nun auch noch die Mächtigkeiten der Schnitte berechnen. Wir definieren daher
\(I_{ab} = I_a \cap I_b, I_{abc} = I_a \cap I_b \cap I_c\) etc.
Jetzt brauchst du nur etwas Konzentration und Ausdauer und erhältst:
\(|I_{ab}| = 3\cdot 4!,\,|I_{ac}| = 2\cdot 4!,\,|I_{ad}| = 5\cdot 4!,\,\)
\(|I_{bc}| = 2\cdot 4!,\,|I_{bd}| = 6\cdot 4!,\,|I_{cd}| = 2\cdot 4!,\,\)
\(|I_{abc}| = 3\cdot 3!,\,|I_{abd}| = 7\cdot 3!,\,|I_{acd}| = 3\cdot 4!,\,|I_{bcd}| = 4\cdot 3!,\,\)
\(|I_{abcd}| = 4\cdot 2!\)
Die von dir gesuchte Funktionenmenge ist
\(\bar I_a \cap \bar I_b \cap \bar I_c \cap \bar I_d = \overline{I_a \cup I_b \cup I_c \cup I_d} = I \setminus (I_a \cup I_b \cup I_c \cup I_d)\)
Jetzt können wir die Inklusion-Exklusion-Formel anwenden:
\(|\bar I_a \cap \bar I_b \cap \bar I_c \cap \bar I_d| = |I| - |I_a \cup I_b \cup I_c \cup I_d|\)
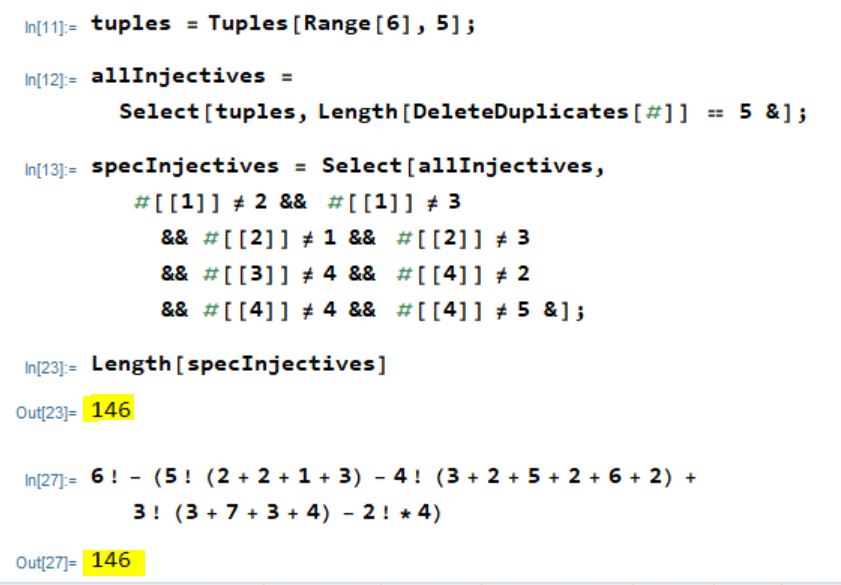
\(= 6!-(5!(2+2+1+3)-4!(3+2+5+2+6+2)+3!(3+7+3+4)-2!\cdot 4)=\boxed{146}\)
Ich hänge hier noch die Verifizierung des Ergebnisses mit Mathematica ran: