Aufgabe:
Bei einem Drehzylinder wird der Radius des Grundkreises mit r und die Höhe des Zylinders mit h bezeichnet. Ist die Höhe des Zylinders konstant, dann beschreibt die Funktion V mit
V (r)=r².π.h die Abhängigkeit des Zylindervolumens vom Radius.
Problem/Ansatz
Im nachstehenden Koordinatensystem ist der Punkt P=(r₁/V(r₁)) eingezeichnet. Ergänzen sie in dem Koordinatensystem den Punkt Q=(3.r₁/V(3.r₁))!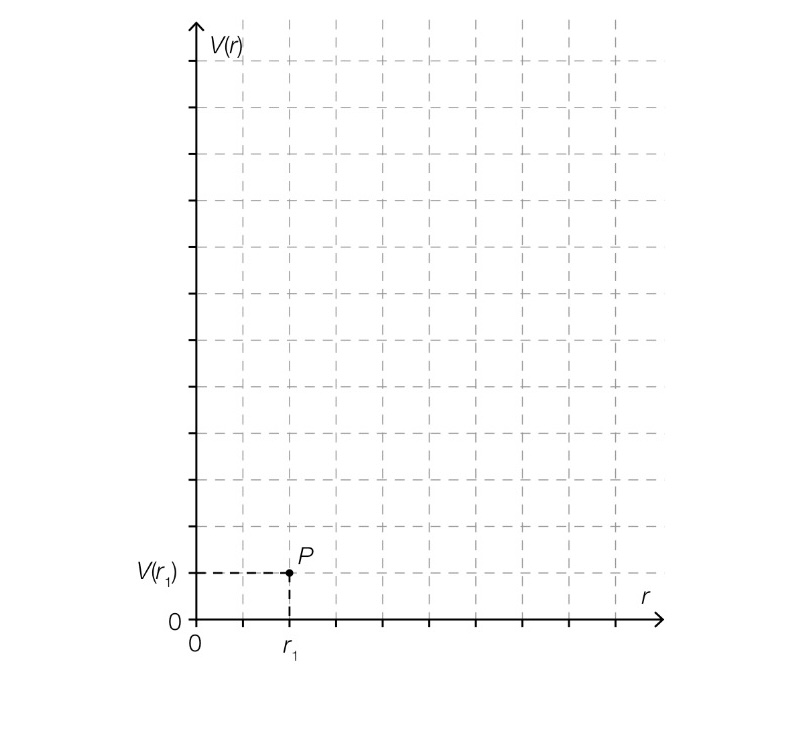
Text erkannt:
\( L \)