Graphen zeichnen und Ableitungen

Question

In der Medizin wir eine Reaktionsstärke R auf ein Medikament in Abhängigkeit von der Dosis d durch die Funktion R mit R(d)= -o,5d^3+2d^2 beschrieben. Die Empfindlichkeit eines Körpers auf die Dosis d wird als die momentane Änderungsrate R´(d) festgelegt.

a) Skizziere die Graphen von R bzw. von R´

b) Für welche Dosis ist die Reaktionsstärke am grössten? Für welche Dosis ist die Empfindlichkeit am grössten?

Würdet ihr bei der a immer Punkte einsetzen?
Wie geht man die Aufgabe b an?

Answer 1

Nochmal hi Simon ;).

 

a) Genau. Würde da wohl auch eine Wertetabelle anlegen ;).

Sieht bei mir so aus:

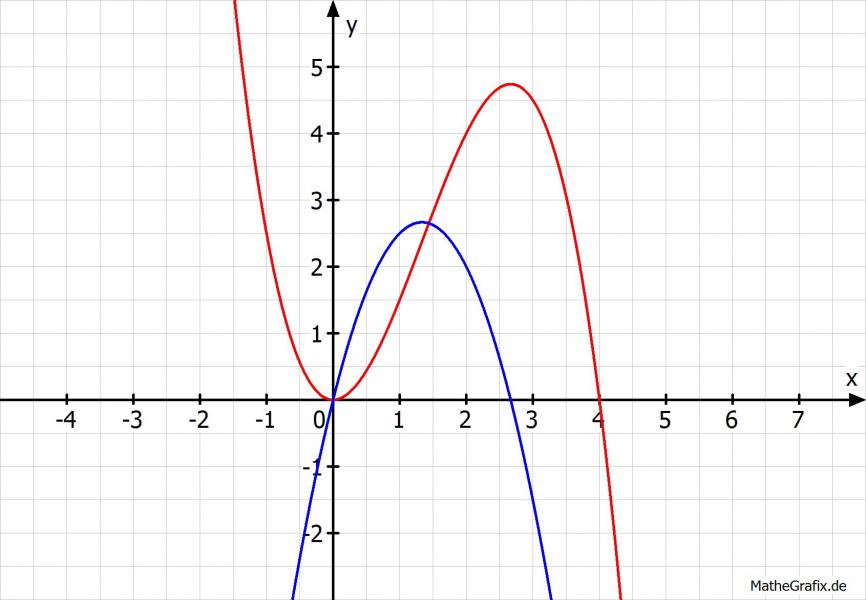
Blau ist die Ableitung.

 

b) "größte Reaktionsstärke" findet man über das Maximum von R(d).

"größte Empfindlichkeit" entspricht der Wendestelle, da die Empfindlichkeit über R'(d) beschrieben wird und das Extremum von R'(d) gebraucht wird. Das entspricht der Wendestelle von R(d).

 

Reaktionsstärke:

R'(d) = -3/2*d^2+4d = 0

d(-3/2d+4) = 0

d₁ = 0

d₂ = 8/3

Nun noch überprüfen (mit zweiter Ableitung) welcher der beiden Punkte das Maximum ist.

Das ist für d₂ der Fall.

 

Empfindlichkeit:

R''(d) = -3d+4 = 0

d = 4/3

Noch überprüfen mit der dritten Ableitung, ob es sich wirklich um eine Wendestelle handelt.

Das ist der Fall.

 

Nun nur noch sauber eine Antwort formulieren ;). Alles klar?

 

Grüße

Comments

Mir ist schonmal klar wie du auf d1 kommst und kann das auch nachvollziehen. Wie kommst du aber auf d2= 8/3? Vielleicht kannst du das ja noch ein wenig detaillierter machen. Bei der Empfindlichkeit verstehe ich deine Vorgehensweise aber wie kommst du von der FG: R´´(d)=-3d+4=0 plötzlich auf die Punkte d=4/3? Deine Vorgehensweise mit den Wendestellen etc. ist mir aber klar. Danke :-)

---

Sry, da war ich etwas schreibfaul ;).

Du musst das nur lösen:


d(-3/2d+4) = 0

Hier gilt der Satz vom Nullprodukt. Entweder ist der erste Faktor 0, oder der zweite.

Für den zweiten:

-3/2d+4 = 0   |+3/2d

3/2d = 4         |*2 /3

d = 8/3


Genauso beim zweiten:

-3d+4 = 0  |+3d

3d = 4        |:3

d = 4/3


Klar?

---

Woher weiss man den ob es 4/3 oder 3/4 sind? Das selbe bei 8/3 oder 3/8? 

Wieso rechnest du nicht bei

-3d+4 =0 |-4

-3d=-4 |-3 gemacht? Wir hatten diesen Satz vom Nullprodukt halt noch nicht. Gruß

                  

---

Das ist doch dasselbe ;).

Also wenn Du |:(-3) meinst.


Da spielt der "Satz vom Nullprodukt" übrigens keine Rolle. Ohnehin kann es sein, dass ihr ihn einfach benutzt ohne ihn zu benennen ;).

---

Stimmt du hast recht! Aber woher weiss man ob 3/4 oder 4/3? Ist der Faktor vor dem d immer das x und die andere Seite das y?

---

Salopp gesagt ja. Zumindest, wenn ich Dich richtig verstehe.

Du weißt schon, dass Punkt- vor Strichrechnung gilt?

Ich muss also zuerst die 4 auf die andere Seite bringen und dann durch den Vorfaktor divideren, damit d alleine steht (was wir ja wollen).

---

Ja punkt vor strich..davon hab ich schonmal was gehört ;-) Scherz! Kenne ich natürlich! Wollte halt nur wissen, da 3d=4 und 4=3d das selbe nur anders herum aufgeschrieben ist wissen, ob der Faktor oder verallgemeinert die Zahl vor dem d der Zähler in unserer Lösung ist.

---

Es macht keinen Unterschied ob Du hast 3d = 4 oder 4 = 3d.
Da da ein Gleichheitszeichen dazwischen ist, bedeutet das, dass beides dasselbe ist. Dürfen also die Seite tauschen. Deine Aufgabe ist es d zu isolieren. Ob dabei d rechts oder links steht ist wurscht. Nur muss durch den Vorfaktor von d dividiert werden. Also durch 3 ;).

---

Also ist doch die Lösung d= 0,75

---

Nein?


4 = 3d   |:3

4/3 = d

d = 1,3333

---

Sry, Denkfehler ;-)Im übrigen! Lange nicht mehr so kompetente und verständliche Erklärungen gehört!  

---

Danke für das Kompliment. Gerne ;).

---

Eine Frage hätte ich da noch. Soll ich sie hier in die Kommentare schreiben oder einfach eine neue Frage machen? Gruß

---

Komplett neue Fragen bitte eigenständig ;).

---

Ok, hab sie gestellt.

---

Hey Simon98!

woher hast du diese Aufgabe her ?

Aus welchem Buch oder Arbeitsheft stammt diese Aufgabe?