Aufgabe:
Text erkannt:
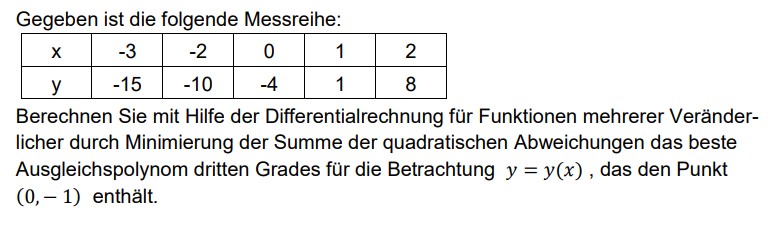
Gegeben ist die folgende Messreihe:
\begin{tabular}{|c|c|c|c|c|c|}
\hline\( x \) & -3 & -2 & 0 & 1 & 2 \\
\hline\( y \) & -15 & -10 & -4 & 1 & 8 \\
\hline
\end{tabular}
Berechnen Sie mit Hilfe der Differentialrechnung für Funktionen mehrerer Veränderlicher durch Minimierung der Summe der quadratischen Abweichungen das beste Ausgleichspolynom dritten Grades für die Betrachtung \( y=y(x) \), das den Punkt \( (0,-1) \) enthält.
Problem/Ansatz:
Hallo. Ich habe eine Frage zu der hinreichenden Bedingung für die Extrema der resultierenden Funktion:
Man hat dann eine Funktion mit drei Variablen g(a,b,c). Wir hatten immer nur Beispiele für Funktionen mit zwei Variablen, bzw. einen Polynom zweiten Grades. Dabei muss man die partielle Ableitung 2. Ordnung bilden und berechnet dann die Diskriminante. Aber wie sieht das bei einer Funktion mit drei Variablen, bzw. einem Polynom 3. Grades aus?
Zudem ist jede partielle Ableitung 3. Ordnung 0, falls das wichtig ist.
Gruß und danke schonmal für die Hilfe ^^
Dasamflo