Zeigen Sie, dass 1/x integrierbar ist und bestimmen Sie dass Integral in den Grenzen von 0 bis b.

Question

Aufgabe: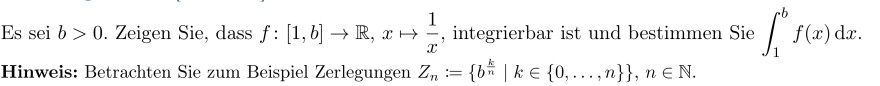

Text erkannt:

Es sei \( b>0 \). Zeigen Sie, dass \( f:[1, b] \rightarrow \mathbb{R}, x \mapsto \frac{1}{x} \), integrierbar ist und bestimmen Sie \( \int \limits_{1}^{b} f(x) \mathrm{d} x \).
Hinweis: Betrachten Sie zum Beispiel Zerlegungen \( Z_{n}:=\left\{b^{\frac{k}{n}} \mid k \in\{0, \ldots, n\}\right\}, n \in \mathbb{N} \).

Problem/Ansatz:

Ich hab ein Problem bei dieser Aufgabe. Ich finde weder nen passenden Ansatz noch hab ich eine Idee wo ich anfangen soll. Für Hilfe wäre ich dankbar.

Answer 1

Stelle Terme für Ober- und Untersumme auf.

Zeige dass Ober- und Untersumme für \(n\to\infty\) gegen \(\ln b\) konvergieren.