Wie haben die in den Lösungen diese Aufgabe berechnet? Es macht doch irgendwie keinen Sinn. Kann mir da jemand weiter helfen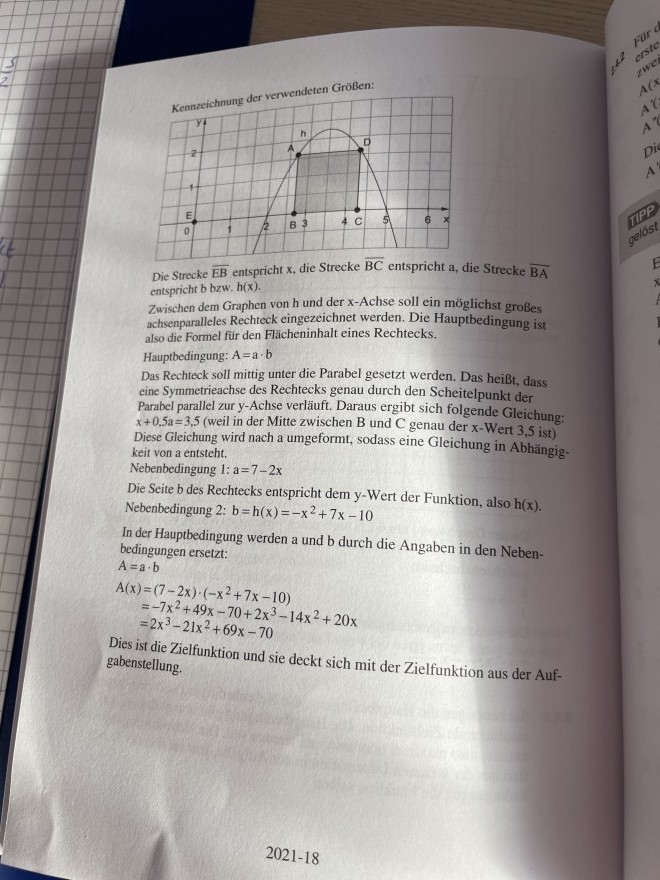
Text erkannt:
Kennzeichnung der verwendeten GröBen:
Die Strecke \( \overline{\mathrm{EB}} \) entspricht \( x \), die Strecke \( \overline{\mathrm{BC}} \) entspricht a, die Strecke \( \overline{\mathrm{BA}} \) entspricht b bzw. \( h(x) \).
Zwischen dem Graphen von h und der x-Achse soll ein möglichst großes achsenparalleles Rechteck eingezeichnet werden. Die Hauptbedingung ist also die Formel für den Flächeninhalt eines Rechtecks.
Hauptbedingung: \( A=a \cdot b \)
Das Rechteck soll mittig unter die Parabel gesetzt werden. Das heißt, dass eine Symmetrieachse des Rechtecks genau durch den Scheitelpunkt der Parabel parallel zur \( y \)-Achse verläuft. Daraus ergibt sich folgende Gleichung: \( x+0,5 \mathrm{a}=3,5 \) (weil in der Mitte zwischen B und C genau der \( \mathrm{x} \)-Wert 3,5 ist) Diese Gleichung wird nach a umgeformt, sodass eine Gleichung in Abhängigkeit von a entsteht.
Nebenbedingung \( 1: \mathrm{a}=7-2 \mathrm{x} \)
Die Seite b des Rechtecks entspricht dem y-Wert der Funktion, also \( h(x) \). Nebenbedingung 2: \( b=h(x)=-x^{2}+7 x-10 \)
In der Hauptbedingung werden a und \( b \) durch die Angaben in den Nebenbedingungen ersetzt: \( \begin{aligned} A(x) & =a \cdot b \\ & =-7-2 x) \cdot\left(-x^{2}+7 x-10\right) \\ & =2 x^{3}-21 x^{2}+69 x-70+2 x^{3}-14 x^{2}+20 x\end{aligned} \)
Dies ist die Zielfunktion und sie deckt sich mit der Zielfunktion aus der Aufgabenstellung.
2021-18