Die Tangente an den Graphen von f im Punkt P bestimmen

Question

Hallo :) Wie bestimme ich die Tangente an den Graphen von f im Punkt P P(x0|f (x0))?
A) f (x)=x^4 & x0=0.5
B) f (x)=2x^-2 & x0=3
C) f (x)=2x^3 -3x^2 & x0=0.5
D) f (x)=x1/x-x^3/2 & x0=5
Danke :)

Answer 1

A) f (x)=x⁴ & x0=0.5

Ich mache das hier mal nur für A vor, weil das vorgehen immer das Gleiche ist.

Du bestimmst die Ableitung der Funktion

f'(x) = 4x^3

Für x0 = 0.5 bestimmst du

f(x0) = f(0.5) = 0.0625

f'(x0) = f'(0.5) = 0.5

Dann stellst du die Tangentengleichung auf

t(x) = f'(x0) * (x - x0) + f(x0) = 0.5 * (x - 0.5) + 0.0625

Fertig. Probier das jetzt mal für die anderen Funktionen alleine.

 

B) f (x)=2x^-2 & x0=3

C) f (x)=2x³ -3x² & x0=0.5

D) f (x)=x1/x-x³/2 & x0=5

Answer 2

 

zunächst erinnert man sich an die allgemeine Geradengleichung

y = mx + b

wobei m die Steigung ist und b der y-Achsenabschnitt

Dies wird jetzt leicht modifiziert in

t(x) = f'(x₀) * (x - x₀) + f(x₀)

denn die Tangente an f(x) hat an der Stelle x₀ den gleichen Anstieg und den gleichen Funktionswert wie f(x) selbst.

Dann setzt man nur noch ein:

 

A)

f(x) = x⁴ ; x₀ = 0,5

f'(x) = 4x³ ; f'(0,5) = 0,5 ; f(0,5) = 0,0625

t(x) = 0,5 * (x - 0,5) + 0,0625

 

B)

f(x) = 2x^-2 ; x₀ = 3

f'(x) = -4x^-3 ; f'(3) = -4/27 ; f(3) = 2/9

t(x) = -4/27 * (x - 3) + 2/9

 

Die anderen analog :-)

 

Besten Gruß

Comments

Danke erstmal! Die ersten beiden habe ich genauso und bei C) habe ich t (x)=-1.5*(x-0.5)-0.5. D) verstehe ich jedoch schon wieder nicht, da ich nicht mit dem 1/x am Anfang umzugehen weiß. Lg!

---

Gern geschehen :-)

Bin gerade erst wieder zu Hause angekommen, ich schaue mir die anderen Teilaufgaben im Laufe des Abends noch an und poste die Lösungen als weiteren Kommentar!

---

 

hier der Rest vom Schützenfest :-D

 

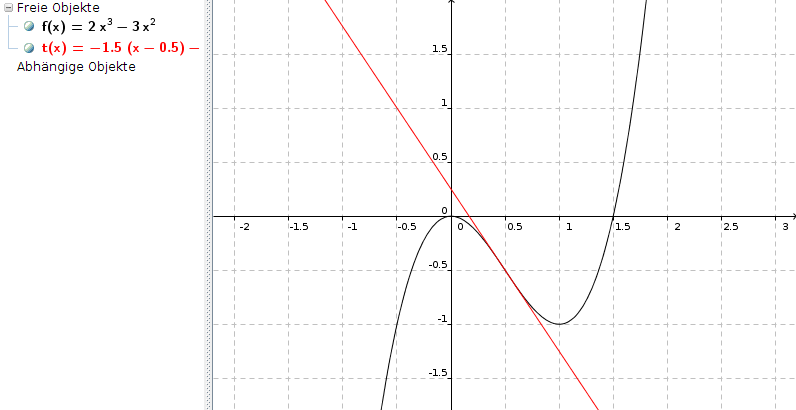
C) f(x)=2x³ - 3x² ; x₀=0,5

f'(x) = 6x² - 6x ; f'(0,5) = 1,5 - 3 = -1,5

f(0,5) = -0,5

Damit ist

t(x) = -1,5 * (x - 0,5) - 0,5 - genauso, wie Du es berechnet hast, prima!!

 

D) f(x) = 1/x - x³/2 ; x₀=5

Meinst Du diese Funktion?

Damit verfahren wir wie gehabt, nachdem wir sie umformuliert haben in 

f(x) = x^-1 - x³/2 {denn 1/x = x^-1}

f'(x) = -x^-2 - 3x²/2

f'(5) = -5^-2 - 75/2 = - 1/25 - 75/2 = -37,54

f(5) = -62,3

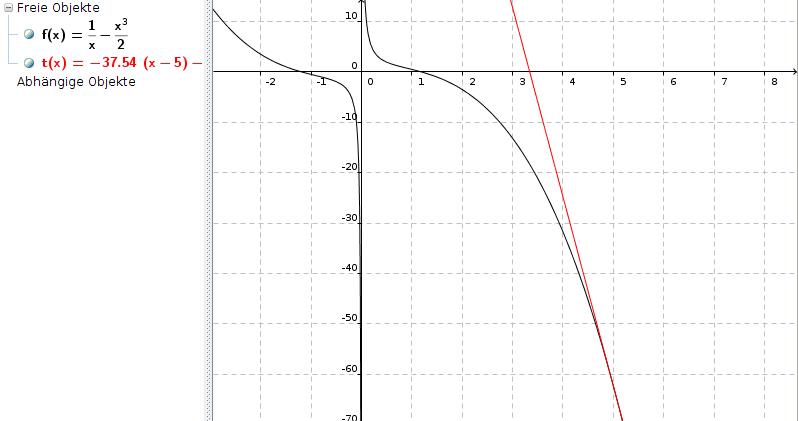
t(x) = -37,54 * (x - 5) - 62,3

Das sieht dann in etwa so aus (Achtung: x- und y-Achse in dieser Skizze unterschiedlich skaliert):

Besten Gruß