Bestimmen Sie den Flächeninhalt des Dreiecks, dass die Tangente an den Graphen von f im Punkt P(x₀|f(x₀)) mit der …

Question

Aufgabe:

Bestimmen Sie den Flächeninhalt des Dreiecks, dass die Tangente an den Graphen von f im Punkt P(x₀|f(x₀)) mit der Geraden n und der x-Achse einschließt.

f(x)= 0,5x² + 2

x₀=2

n(x)= −0,5x + 5

Answer 1

Wie man Gleichungen von Tangenten bestimmt, siehst du in den Antworten zu einer deiner anderen Fragen. Ebenfalls wie man den Schnittpunkt von \(n\) und der Tangente berechnet.

Formel für den Flächeninhalt eines Dreiecks ist

        \(\text{Flächeninhalt}=\frac{1}{2}\cdot\text{Grundseite}\cdot\text{Höhe}\).

Comments

Was mache ich, wenn ich die Tangente und n berechnet habe?

Was ist g und was ist h

---

Was mache ich, wenn ich die Tangente und n berechnet habe?

Schnittpunkt berechnen. Das ist eine Ecke des Dreiecks.

Was ist g und was ist h

In der Formel für den Flächeninhalt ist g eine Seite des Dreicks und h die dazu passende Höhe (das heißt sie verläuft von der g gegenüberliegenden Ecke senkrecht auf die Gerade, in der g liegt).

Answer 2

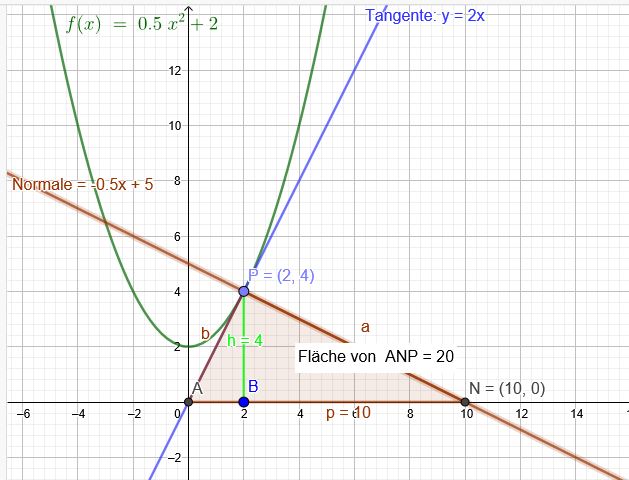
Bestimmen Sie den Flächeninhalt des Dreiecks, dass die Tangente an den Graphen von f im Punkt P(2|f(x₀)) mit der Geraden n und der x-Achse einschließt.

\(f(x)= 0,5x^2 + 2 \)       \(f(2)= 4 \)        P\((\blue{2}|\red{4}))\)
\(n(x)= −0,5x + 5\)

\(f'(x)=x \)    \(f'(2)=\orange{2} \)

Berechnung der Tangente:

\( \frac{y-\red{4}}{x-\blue{2}}= \orange{2}\)

\( y=2x\) geht durch den Ursprung → Flächenberechnung

Schnitt der Tangente \( y=2x\)  mit  \(n(x)= −0,5x + 5\)

\(2x= −0,5x + 5\)

\(x=\blue{2}\)  \( y=\red{4}\)

Es existiert ein rechter Winkel zwischen \( y=2x\) und \(n(x)= −0,5x + 5\), weil

\(2\cdot (-0,5)=-1\) ist

Die Normale \(n(x)= −0,5x + 5\)schneidet die x-Achse in N\((10|0)\)

Fläche des Dreiecks \( A=\frac{1}{2}\cdot 10\cdot \red{4}=20  \)