Was ist der längste Weg, den man in diesem 3×4-Gitter aus Zündhölzchen durch Wegnehmen der Zündhölzchen gehen kann?

Question

Aufgabe:

Was ist der längste weg, den man in diesem 3x4-Gitter aus Zündhölzchen durch wegnehmen der Zündhölzchen gehen kann? Aus 31 Hölzchen wurde dieses Gitter gelegt

Spielregel:

Nimm eine fortlaufende Reihe von möglichst vielen Hölzchen weg. Die Reihe soll sich wie im Beispiel als fortlaufende Hölzchenschlange durch die Figur schlängeln. Abbiegen und überkreuzen ist erlaubt.

Lösung:

Der maximale zusammenhängende Weg, den man erzeugt, indem man Hölzchen aus dem Gitter nimmt ist 27 Hölzchen lang.

Problem/Ansatz:

Ich weiss, dass es ein Problem aus der Graphentheorie (die ich nicht kenne) ist, das ist aber eine "Knobelaufgabe" für Kinder aus der sechsten Klasse. Nun frage ich mich folgende Fragen:

A) Gibt es eine allgemeine Regel wie ich aus der Anzahl Hölzchen (oder Anzahl Zeilen und Spalten) ableiten kann, was der längste Weg ist ?

B) Weiss jemand, welche didaktische Bedeutung so eine Aufgabe haben kann ?

C) Ist die Spielregel gleichbedeutend mit der Aussage, dass ein Weg nicht zwei mal begangen werden darf? Also heisst "Abbiegen und Kreuzen erlaubt" auch dass ein Weg nicht zwei mal begangen werden darf ?

Vielen Dank im Voraus!

Answer 1

Hallo,

Gibt es eine allgemeine Regel wie ich aus der Anzahl Hölzchen (oder Anzahl Zeilen und Spalten) ableiten kann, was der längste Weg ist ?

es gibt eine allgemeine Regel, die aber nicht auf die Anzahl Hölzchen sondern auf die Anzahl der Kanten an jedem Knoten abzielt. Ein Knoten ist dort wo sich zwei oder mehr Hölzchen treffen und jedes Hölzchen ist eine Kante.

Als ich in der sechsten Klasse war, haben wir ein ähnliches Spielchen mit dem berühmten Haus vom Nikolaus gespielt. Das ist allerdings etwas einfacher. Aber auch (wir) Kinder kommen da ziemlich schnell drauf, dass nur die Knoten als "innere Knoten" der Schlange taugen, wenn die Anzahl der Kanten (hier die Hölzchen) gerade ist.

Bezogen auf diese konkrete Aufgabe heißt das, dass man durch Wegnehmen von Hölzchen aus möglichst vielen Knoten mit ungeradem Grad (so heißt die Anzahl in 'Graphen-Deutsch') einen mit geraden Grad machen muss, so dass am Ende nur zwei ungerade für Start und Ende übrig bleiben. Hier eine mögliche Lösung:

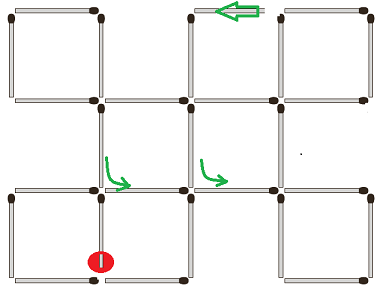
Start beim grünen Pfeil und dann immer "geradeaus", und nur zweimal Abbiegen, da wo es angeschrieben steht.

B) Weiss jemand, welche didaktische Bedeutung so eine Aufgabe haben kann ?

Was ist eine 'didaktische Bedeutung'? Die Aufgabe taugt für Kinder, weil sie keinerlei mathematisches Vorwissen erfordert. Trotzdem enthält sie alles was man einem 'mathematischen Problem' so abverlangen kann. Man kann zunächst viel herum probieren um (hoffentlich) irgendwann zu logischen Schlussfolgerungen, Gesetzmäßigkeiten und schlußendlich zu einer Lösung zu kommen.

C) Ist die Spielregel gleichbedeutend mit der Aussage, dass ein Weg nicht zwei mal begangen werden darf? Also heisst "Abbiegen und Kreuzen erlaubt" auch dass ein Weg nicht zwei mal begangen werden darf ?

Ja - genau das. Und das wäre auch mein Kritikpunkt an der Aufgabenstellung. Genau diese Anforderung "kein Hölzchen darf zweimal für die Schlange benutzt werden" sollte klarer formuliert werden. Aber vielleicht ist das den Kindern implizit klar, wenn man von einer "Schlange" spricht. Da geht das ja auch nicht ;-)

Gruß Werner

Comments

Wow, vielen Dank für deine Ausführungen !

Interessant. Wenn du Zeit und Gelegenheit hast, könntest du bitte noch sagen, was genau mit den "inneren Knoten" gemeint/voreilhaft ist?

Ich habe mit einem Freund diskutiert, ob es sinnvoll ist di eKnoten zu brauchen, die ganz am Rande sind, er meinte nein.

Ist es das, was du mit den inneren Knoten meinst ?

---

... könntest du bitte noch sagen, was genau mit den "inneren Knoten" gemeint/voreilhaft ist

Zitat aus der Aufgabestellung:

Die Reihe soll sich wie im Beispiel als fortlaufende Hölzchenschlange durch die Figur schlängeln

Da unterstelle ich mal ganz naiv, dass das z.B. so aussehen könnte:

eine Hölzchenschlange ergibt sich wenn man Hölzchen an Hölzchen legt. Und jeder Kontaktpunkt ist ein "innerer Knoten". 'Innen' deshalb, weil die Schlange hier noch nicht zu Ende ist. (die rot markierten Stellen). Man kann sich vorstellen, dass mit Verfolgung der blauen Spur im Bild daraus eine Schlange wird.

Und damit das so aufgeht, müssen an jedem "inneren Knoten" ein geradzahlige Anzahl von Hölzchen anliegen. Mindestens 2 oder wenn sich eine Kreuzung ergibt, ein Vielfaches davon.

Weiterhin muss es genau zwei oder keinen - dann beißt sich die Schlange in den Schwanz - Knoten mit ungeradem Grad geben, Also mit einer ungeraden Anzahl von Hölzchen. Sonst sind entweder Hölzchen über oder es gibt mehr als eine Schlange.

Ich habe mit einem Freund diskutiert, ob es sinnvoll ist die Knoten zu brauchen, die ganz am Rande sind, er meinte nein.
Ist es das, was du mit den inneren Knoten meinst ?

Solltest Du jetzt selbst beantworten können ;-)

---

Achsoooo. Ja, klar! :-)

Vielen Dank !