Aufgabe:
Es ist der Graph \( G=(V, E) \) durch das folgende Diagramm gegeben:
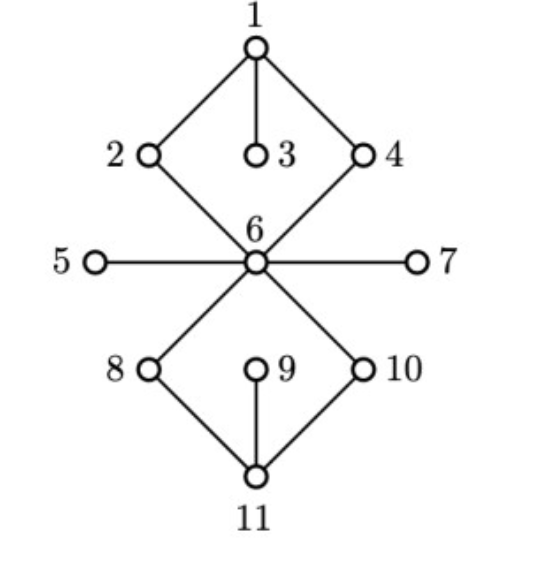
Für welches maximale \( k \in \mathbb{N} \) ist \( G k \)-fach zusammenhängend? Begründen Sie Ihre Antwort! Geben Sie alle Blöcke von \( G \) jeweils durch ein Diagramm an. Geben Sie für den Blockgraphen \( G_{B} \) von \( G \) seine Knotenmenge \( V_{B} \) und seine Kantenmenge \( E_{B} \) an und zeichnen Sie ein Diagramm dieses Blockgraphen.
Begründen Sie, dass mindestens drei Kanten zu \( G \) hinzugefügt werden müssen (unter Beibehaltung der Knotenmenge), damit der Blockgraph des so erzeugten Graphen aus genau einem isolierten Punkt besteht. Geben Sie drei Kanten an, mit denen das gelingt.
Problem/Ansatz:
Bei der ersten Aufgabe habe ich, dass es 1 fach zusammenhägend ist, weil bei 2 fach zusammenhägend, wenn ich die Kante zwischen 1 und 3 entferne, ist der Knoten 3 fei ohne eine eine Kantenverbindung, und deshalb wäre es nicht 3 fachzusammenhägend.
Bei Aufgabe 2 habe die Blöcke :
Block 1: {1,3}
Block 2: {1,2,4,6}
Block 3: {6,5}
Block 4: (6,7)
Block 5: {6,8,10,11}
Block 6: {11,9}
1, 6 und 11 sind die Gelenkpunkte.
V={B1,B2,B3,B4,B5,B6,1,6,11}
\( E_{B} \={{B1,1},{1,B2},{B2,6},{6,B3},{6,B4},{6,B5}{B5,11}{11,B6}}
Aufgabe 3:
Die Begründung hierfür ist, dass jeder Block ein maximale zusammenhängender Teil des Graphen ist. Um den Blockgraph auf einen isolierten Punkt zu reduzieren, muss jeder Knoten in einem eigenen Block sein. Das bedeutet, dass jeder Knoten nur mit sich selbst verbunden sein muss, und keine Kanten zwischen den Knoten vorhanden sein dürfen.
Um dies zu erreichen, müssen mindestens drei Kanten hinzugefügt werden, da jeder Knoten mindestens eine Kante hat.
Die mindestens drei Kanten, die hinzugefügt werden können, sind beispielsweise:
(1, 1), (2, 2), (3, 3)
(1,1), (2,2), (4,4)
(5,5), (6,6), (7,7)
Diese Kanten erstellen in G eine Art "Schleife" jeder Knoten ist mit sich selbst verbunden und so keine Kanten zwischen Knoten existieren. Der Blockgraph von G würde dann aus genau einem isolierten Punkt bestehen.
Könnte mir jemand helfen, ob ich die Aufgaben 1 und 2 richtig gelößt habe, wenn nicht ob mir dann jemand seine Lösung schrieben könnte. Kann mir jemand bei Aufgabe 3 sagen, ob die Idee riicthig ist, wenn nicht ob mir dann jemand seine Idee schreiben kann. ich würde mich richtig freuen, wenn ihr mir dabei helfen könntet