Aufgabe:
Wie beweist man die Konvergenz dieser Folge?
Problem: Ist mein Ansatz korrekt?
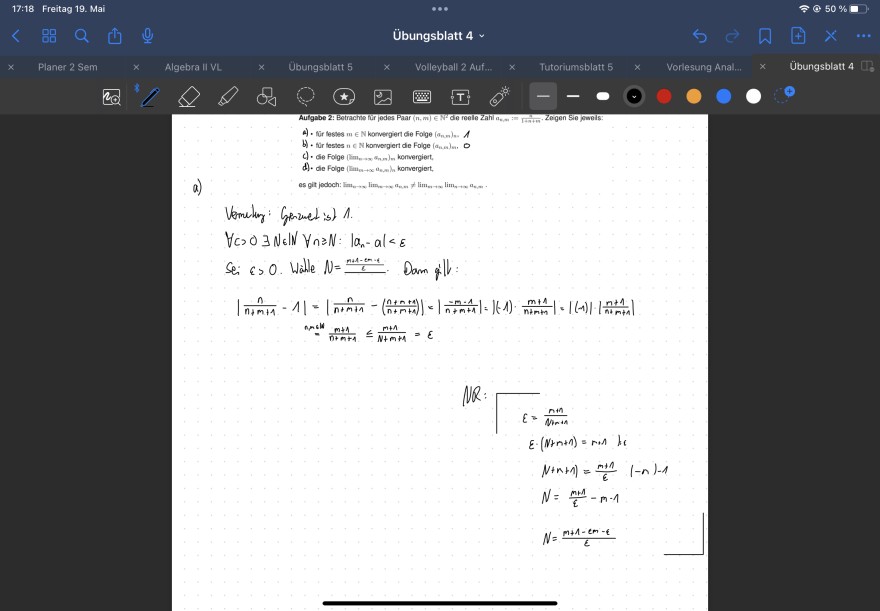
Text erkannt:
17:18 Freitag 19. Mai
8
(이
Übungsblatt 4 v
Planer 2 Sem
\( x \)
a)
A) . für lesses m \( \in \) N kacvergiert die Folge \( \left(a_{n-n}\right)_{n-} A \)
b) + für festes a \( \in \) N komergiert de Folge \( \left(a_{n, 6}\right)_{\text {men }}, D \)
c) - die Folge (limn was tnn \( _{\text {n m }} \) konvergiert.
es git jedoch: \( \operatorname{lin}_{\mathrm{w} \rightarrow \infty} \lim \limits_{n-\infty} a_{n, n} \neq \lim \limits_{n \rightarrow \infty} \lim \limits_{n \rightarrow \infty} a_{n, w} \).
Vemeter: Genzed ist 1.
\( \forall c>0 \exists \mathbb{N} \in \mathbb{N} \quad \forall n \geqslant N:\left|a_{n}-a\right|<\varepsilon \)
\( \begin{array}{c} \left|\frac{n}{n+m+1}-1\right|=\left|\frac{n}{n+m+1}-\left(\frac{n+m+1}{n+n+1}\right)\right|=\left|\frac{-m-1}{n+m+1}\right|=\left|(-1) \cdot \frac{m+1}{n+m+1}\right|=|(-1)| \cdot\left|\frac{m+1}{n+m+1}\right| \\ n=\frac{m+1}{n+m+1} \leq \frac{m+1}{n+m+1}=\varepsilon \end{array} \)
\( \begin{array}{l} N R= \\ \varepsilon= \frac{n+1}{\operatorname{Mim+1}} \\ \varepsilon \cdot(N+n+1)=m+1 \quad k i \\ N+n+1)=\frac{m+1}{\varepsilon}(-n)-1 \\ N=\frac{m+1}{\varepsilon}-m-1 \\ N=\frac{m+1-c m-\varepsilon}{\varepsilon} \end{array} \)