Welchen Winkel eta bilden die beiden Diagonalen e und f eines Parallelogramms ABCS miteinander, wenn die Seite a …

Question

Aufgabe:

Welchen Winkel eta bilden die beiden Diagonalen e und f eines Parallelogramms ABCS miteinander, wenn die Seite a dreimal so lang ist wie die Seite b und die Diagonale e zweieinhalbmal so lang wie die Seite b ist?

Problem/Ansatz:

Hallo,

dies ist eine Übung für unsere Klausur über Trigonometrie und sie lässt mich sehr verzweifeln! Ich habe schon (gefühlt) alles probiert, von Sinus-/Kosinussatz bis Winkelsummensatz und rechtwinkliges Dreieck suchen. Ich schaffe es aber einfach nicht… Könnte mir jemand helfen! Viele, vielen Dank im Voraus!!!!

Answer 1

Nach Kosinussatz gilt

3² = 2.5² + 1² - 2·2.5·1·COS(γ) --> γ = 110.49°

und weiter

(f/2)² = (2.5/2)² + 1² - 2·(2.5/2)·1·COS(110.49°) --> f/2 = 1.854

und damit weiter

1² = (2.5/2)² + 1.854² - 2·(2.5/2)·1.854·COS(ε) --> ε = 30.35°

Skizze

Comments

Vielen, vielen Dank! Sie sind mein Retter!!!

---

Ja, Ihre Antwort hat mir auch geholfen! Vielen Dank! Dennoch versuchen Sie in der Zukunft mehr ausführlicher zu erklären, denn sie reden ohne Subjekt und Prädikat!

Die Seiten, die nach b umgestellt worden sind, versteht man, als ob sie ihren eigenen Wert haben und bei f/2 genauso! Weil f/2 ist 1,854b nicht 1,854!

---

Kleiner Tipp: Da sich Winkel bei einer zentrischen Streckung nicht ändern, kann das Parallelogramm so gestreckt werden, dass die Seite b die Länge 1 erhält. Daher kann man so viel einfacher notieren und so damit rechnen.

D.h. es werden einfach alle Längen als Vielfache von b angegeben. Aber du hast recht. Das sollte man nicht so erfahrenen Schülern vermutlich sagen. Schön, dass du es trotzdem verstanden hast.

---

Ja, danke sehr!

Answer 2

Was willst du denn noch? Mit den Vorgaben sind die Innenwinkel des Dreiecks ABC eindeutig bestimmt.

Im Dreieck ABS (S ist der Diagonalenschnittpunkt) kannst du danach mit dem Kosinussatz f/2=BS ausrechnen.

Answer 3

Arbeitsskizze:

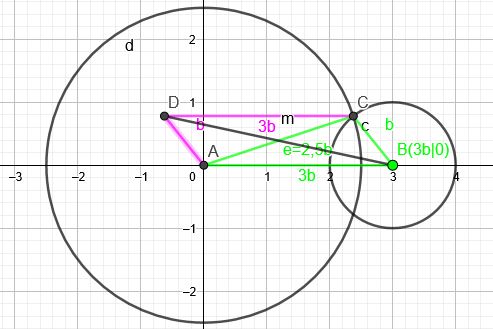
Bestimmung der Koordinaten von C:

Kreis um A  $d: x^2+y^2=6,25b^2$  →    $d: y^2=6,25b^2-x^2$

Kreis um B $c: (x-3b)^2+y^2=b^2$

Schnitt von d und c:

$(x-3b)^2+6,25b^2-x^2=b^2$

$x^2-6bx+9b^2+6,25b^2-x^2=b^2$

$x=\frac{ 14,25b^2}{6b}=2,375b$

$y^2=6,25b^2-(2,375b)^2=0,609375b^2$  $y=0,78062475b$

C$(2,375b|0,78062475b)$

Steigung der Geraden durch A und C:$m_1= \frac{0,78062475b}{2,375b}=0,32868411≈0,33$

Bestimmung der Koordinaten von D:

$x^2+y^2=b^2$   schneidet  $y=0,78062475b$→  $y^2=0,609375b^2$

$x^2+0,609375b^2=b^2$     →  $x^2=b^2-0,609375b^2=0,390625b^2$

$x=-0,625b$$x^{a·b}$

D$(-0,625b|0,78062475b)$

$m_2=\frac{0,78062475b-0}{-0,625b-3b}=-0,21534476≈-0,215$

Allgemeine Formel:

$\tan(ε)=|\frac{m_2-m_1}{1+m_2m_1}|$

$\tan(ε)=|\frac{-0,215-0,33}{1+(-0,215)\cdot 0,33}|≈|-0,59|=0,59$

$\tan^{-1}(0,59)=30,54°$

$ε=30,54°$

Comments

Die Bestimmung der Koordinaten von D ist unnötig kompliziert, das kann man direkt ablesen.

Und Du solltest erklären, warum Dein Ergebnis von dem von mc abweicht.

---

Das könnte mit Rundungsfehlern zusammenhängen. Eine andere Erklärung weiß ich nicht.