Text erkannt:
1. Gegeben ist die Funktionenschar \( f_{k}: D \rightarrow \mathbb{R} ; x \longmapsto \frac{x^{3}}{2(x+k)^{2}}, k \in \mathbb{R} \).
(a) Geben sie die Definitionsmenge \( D \) in Abhängigkeit von \( k \) an und zeigen Sie, dass für alle \( x \in \mathbb{R} \) gilt: \( \quad f_{k}^{\prime \prime}(x)=\frac{3 k^{2} \cdot x}{(x+k)^{4}} \).
(b) Bestimmen Sie die Funktion der Schar, deren Graph an der Stelle-6 einen Extrempunkt hat und die Art des Extrempunktes.
(c) Begründen Sie, ob es ein \( k \in \mathbb{R} \) gibt, für welches die Funktionenschar \( f_{k} \) symmetrisch zur y-Achse oder zum Ursprung ist?
(d) Zeigen Sie: Für jedes \( k \in \mathbb{R}^{*} \) entsteht der Graph der Funktion \( f_{-k} \) aus dem Graphen der Funktion \( f_{k} \) durch Spiegelung am Koordinatenursprung.
2. Diskutieren Sie die Funktion \( f: D \rightarrow \mathbb{R} ; x \longmapsto \ln \frac{4 x}{4-x} \).
(Denken Sie an: Definitionsbereich, Symmetrie, Nullstellen, Extremstellen, Wendestellen, Monotonieverhalten, Grenzverhalten für \( x \rightarrow \pm \infty \), Krünnungsintervalle und Skizze)
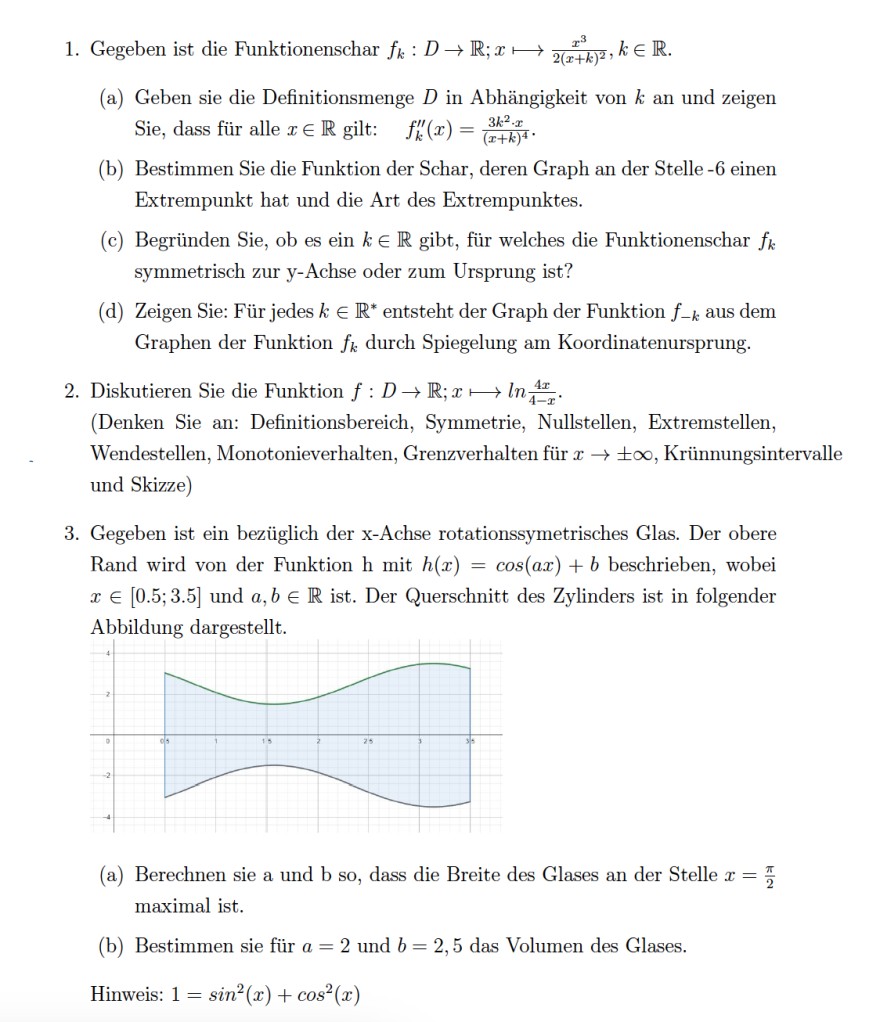
3. Gegeben ist ein bezüglich der \( \mathrm{x} \)-Achse rotationssymetrisches Glas. Der obere Rand wird von der Funktion \( \mathrm{h} \) mit \( h(x)=\cos (a x)+b \) beschrieben, wobei \( x \in[0.5 ; 3.5] \) und \( a, b \in \mathbb{R} \) ist. Der Querschnitt des Zylinders ist in folgender Abbildung dargestellt.
(a) Berechnen sie a und b so, dass die Breite des Glases an der Stelle \( x=\frac{\pi}{2} \) maximal ist.
(b) Bestimmen sie für \( a=2 \) und \( b=2,5 \) das Volumen des Glases.
Hinweis: \( 1=\sin ^{2}(x)+\cos ^{2}(x) \)
Hallo, ich weiß leider gar nicht mit den Aufgaben unzugehen, somit habe nichtmal einen Ansatz und verzweifle langsam.
Kann mir jemand helfen?