Auswirkung von Faktor vor dem x bei einer Potenzreihe

Question

Aufgabe:

Geben Sie zu der folgenden Potenzreihe, bezüglich der allgemeinen Form, jeweils den Koeffizienten a_n, die Entwicklungsstelle x₀ und den zugehörigen Konvergenzradius ρ an:

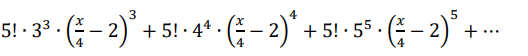
Text erkannt:

\( 5 ! \cdot 3^{3} \cdot\left(\frac{x}{4}-2\right)^{3}+5 ! \cdot 4^{4} \cdot\left(\frac{x}{4}-2\right)^{4}+5 ! \cdot 5^{5} \cdot\left(\frac{x}{4}-2\right)^{5}+\cdots \)

Problem/Ansatz:

Als Bildungsvorschrift aufgestellt habe ich:

\( \sum\limits_{n=3}^{\infty}{} \)5!*nⁿ(\( \frac{x}{4} \) - 2)ⁿ

Der Faktor \( \frac{1}{4} \)  bei dem x verunsichert mich. Wir hatten noch keine Potenzreihe mit einem Faktor vor dem x. Hat der eine Auswirkung auf die Entwicklungsstelle? Und a_n ist nⁿ .

Schonmal danke für die Hilfe :)

Answer 1

\(\left(\frac{x}{4}-2\right)^{n}=\left(\frac{1}{4}\left(x-8\right)\right)^{n}=\frac{1}{4^{n}}\left(x-8\right)^{n}\)

\(a_n=5!\cdot n^n\cdot \frac{1}{4^n}\)

\(x_0 = 8\)

Comments

Vielen Dank!