Aloha :)
Ich habe die Situation mal von WolframAlpha zeichnen lassen:
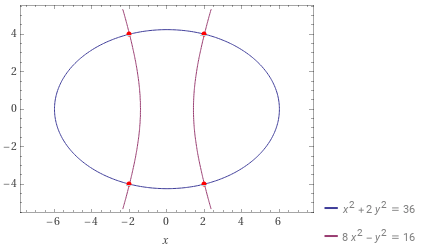
Daraus können wir folgendes Vorgehen ablesen.
1) Wir bestimmen den Schnittpunkt \((x_0|?)\) rechts oben.
2) Wir rotieren die Fläche unter der blauen Kurve im Intervall \([0;x_0]\) um die x-Achse.
3) Wir bestimmen die rechte Nullstelle \((x_1|0)\) der roten Kurve.
4) Wir rotieren die Fläche unter der roten Kurve im Intervall \([x_1;x_0]\) um die x-Achse.
5) Wir subtrahien das zweite Volumen vom ersten Volumen.
Bei der Rotation einer Funktion \(f(x)\) um die \(x\)-Achse entsteht an der Stelle \(x\) ein Kreis um die x-Achse, dessen Mittelpunkt auf der x-Achse liegt. Der Radius dieses Kreises ist gleich dem Funktionswert an der Stelle \(x\), d.h. \(r=f(x)\). Die bei der Rotation entstandene Fläche ist daher \(\pi\,r^2=\pi\,f^2(x)\).
Diese Kreisflächen müssen wir entlang der x-Achse summieren.
Wir fassen das Gesagte formal zusammen:$$V=\int\limits_0^{x_0}\pi f^2_{\text{blau}}(x)\,dx-\int\limits_{x_1}^{x_0}\pi f^2_{\text{rot}}(x)\,dx$$
Für die Funktionsgleichungen formen wir die beiden Kegelschnitt-Gleichugen um:
$$\color{blue}x^2+2y^2=36\implies y^2=\frac{36-x^2}{2}\implies f^2_{\text{blau}}(x)=18-\frac{x^2}{2}$$$$\color{red}8x^2-y^2=16\implies y^2=8x^2-16\implies f^2_{\text{rot}}(x)=8x^2-16$$
Den Schnittpunkt \((x_0\ge0)\) beider Funktion rechts oben im ersen Quadranten erhalten wir durch Gleichsetzen:$$18-\frac{x_0^2}{2}=8x_0^2-16\implies\frac{17}{2}x_0^2=34\implies x_0^2=4\implies x_0=2$$
Die rechte Nullstelle \((x_1\ge0)\) der roten Funktion ist offensichtlich: \(x_1=\sqrt2\).
Damit haben wir alles, um unsere Formel zu konkretisieren:$$V=\pi\int\limits_0^2\left(18-\frac{x^2}{2}\right)dx-\pi\int\limits_{\sqrt2}^2(8x^2-16)\,dx=\pi\left[18x-\frac{x^3}{6}\right]_0^2-\pi\left[\frac83x^3-16x\right]_{\sqrt2}^2$$$$\phantom V=\frac{104}{3}\pi-\frac{32(\sqrt2-1)}{3}\pi=\frac83\pi(13-4(\sqrt2-1))=\frac83\pi(17-4\sqrt2)\approx95,0281$$