Bestimmen Sie den Funktionsterm mit Tangente

Question

Aufgabe:

Funktionsterm bestimmen: Die Funktion zu f(x) = ax³+bx²+ex+d hat bei x = 1/2 eine Nullstelle und eine Wendestelle, die Gleichung der Tangente an den Graphen von f im Punkt P(2/0) ist f(x) = 9x-18.

a) Bestimmen Sie den Funktionsterm.

Problem/Ansatz:

Answer 1

f(1/2) = 0

f''(1/2) = 0

f(2) = 0

f'(2) = f'(2)

Löse das Gleichungssystem.

N. B. in der letzten Gleichung ist das linke f die gesuchte Funktion und das rechte f die Tangente.

Comments

Danke! Warum benötigt man hier f´(2) = fˋ(2) ?

---

Die Tangente von f hat an der Stelle 2 die gleiche Steigung wie f.

Answer 2

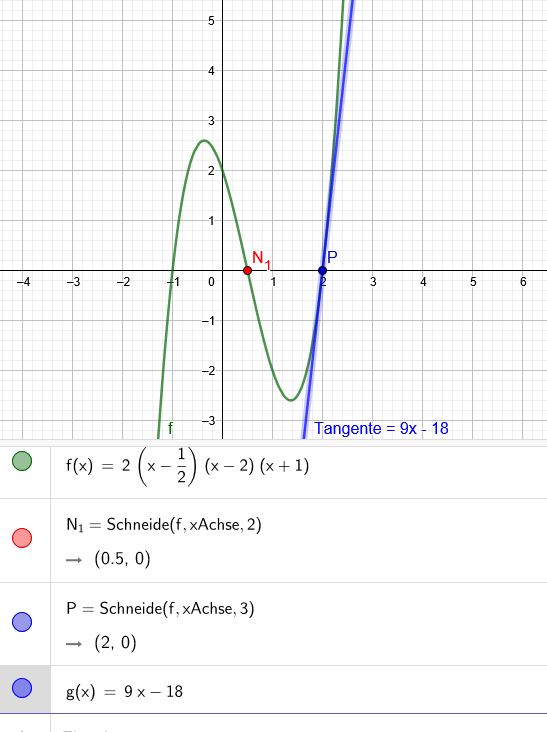
Die Funktion zu \(f(x) = ax^3+bx^2+ex+d\) hat bei \(x = \frac{1}{2} \) eine Nullstelle und eine Wendestelle. Die Gleichung der Tangente an den Graphen von f im Punkt \(P(2|0)\) ist \(g(x) = 9x-18\)

\(f(x)=a*[(x- \frac{1}{2})*(x-2)*(x-N)]\)

\(f´(x)=a*[(x-2)*(x-N)+(x- \frac{1}{2})*(x-N)+(x- \frac{1}{2})*(x-2)]\)

\(f´(2)=a*[(2-2)*(2-N)+(2- \frac{1}{2})*(2-N)+(x- \frac{1}{2})*(2-2)]\)

\(f´(2)=1,5a*(2-N)=9\)    →  \(a=\frac{6}{2-N}\)

\(f´(x)=\frac{6}{2-N}*[(x-2)*(x-N)+(x- \frac{1}{2})*(x-N)+(x- \frac{1}{2})*(x-2)]\)

\(f´´(x)\\=\frac{6}{2-N}*[(x-N)+(x-2)+(x-N)+(x- \frac{1}{2})+(x-2)+(x- \frac{1}{2})]\)

\(f´´(\frac{1}{2})\\=\frac{6}{2-N}*[(\frac{1}{2}-N)+(\frac{1}{2}-2)+(\frac{1}{2}-N)+(\frac{1}{2}- \frac{1}{2})+(\frac{1}{2}-2)+(\frac{1}{2}- \frac{1}{2})]\)

\(f´´(\frac{1}{2})=\frac{6}{2-N}*[(\frac{1}{2}-N)-1,5+(\frac{1}{2}-N)-1,5)]\)

\(f´´(\frac{1}{2})=\frac{6}{2-N}*[(1-2N)-3)]\)

\(f´´(\frac{1}{2})=\frac{6}{2-N}*[-2N-2)]\)

\(\frac{6}{2-N}*[-2N-2)]=0\)  →\(N=-1\)    \(a=\frac{6}{2+1}=2\)

\(f(x)=2*(x- \frac{1}{2})*(x-2)*(x+1)\)