Aufgabe:
Ausgehend von den Daten aus einer Statistik der Vereinten Nationen kann das Durchschnittsalter der Bevölkerung in einem Land A mit Hilfe der Funktion a mit der Gleichung
a(t) = -0,00011 t3 + 0,0186 t2 - 0,538 t + 24, t ∈ ℝ,
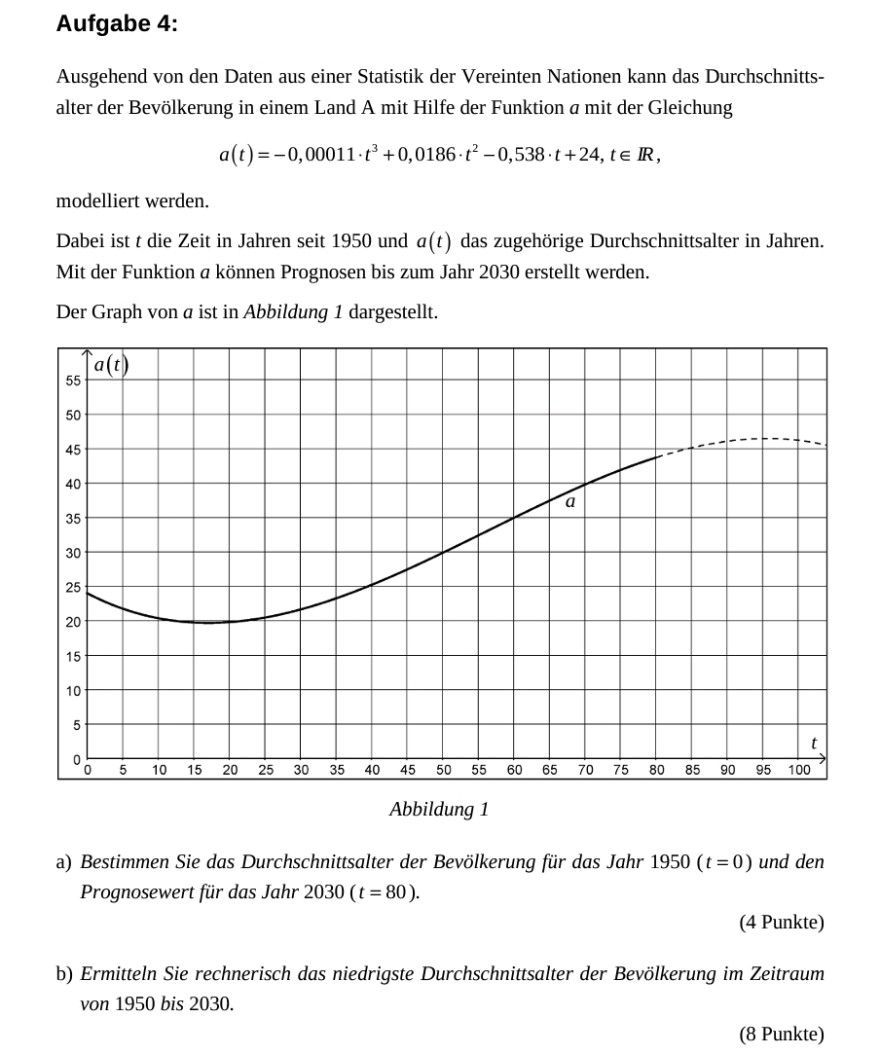
modelliert werden. Dabei ist t die Zeit in Jahren seit 1950 und a(t) das zugehörige Durchschnittsalter in Jahren. Mit der Funktion \( a \) können Prognosen bis zum Jahr 2030 erstellt werden. Der Graph von \( a \) ist in Abbildung 1 dargestellt.
a) Bestimmen Sie das Durchschnittsalter der Bevölkerung für das Jahr \( 1950(t=0) \) und den Prognosewert für das Jahr \( 2030(t=80) \).
b) Ermitteln Sie rechnerisch das niedrigste Durchschnittsalter der Bevölkerung im Zeitraum von 1950 bis 2030
Problem/Ansatz:
Ich verstehe überhaupt nicht wie hier gerechnet werden muss. Also ich habe die Ableitung bereits gemacht. Weiter weiß ich aber nicht