Analysis (Sekante) näherung an punkte ZK

Question

Aufgabe

… Der Nachbarpunkt nähert sich auf dem Funktionsgraphen von f(x)=x^3-7,5x^2+12x-5,5

dem Punkt H(1/0) an. Dadurch nähert sich die Steigung der Sekante durch H und diesen Nachbaepunkt einer Bestimmten Zahl an.

Geben Sie diese Zahl an und begründen Sie, warum sich die Steigung der Sekante der angegebenen Zahl nähert.

Problem/Ansatz:

Keine Ahnung was man machen soll. Aufgabenstellung komplizierter als mein Leben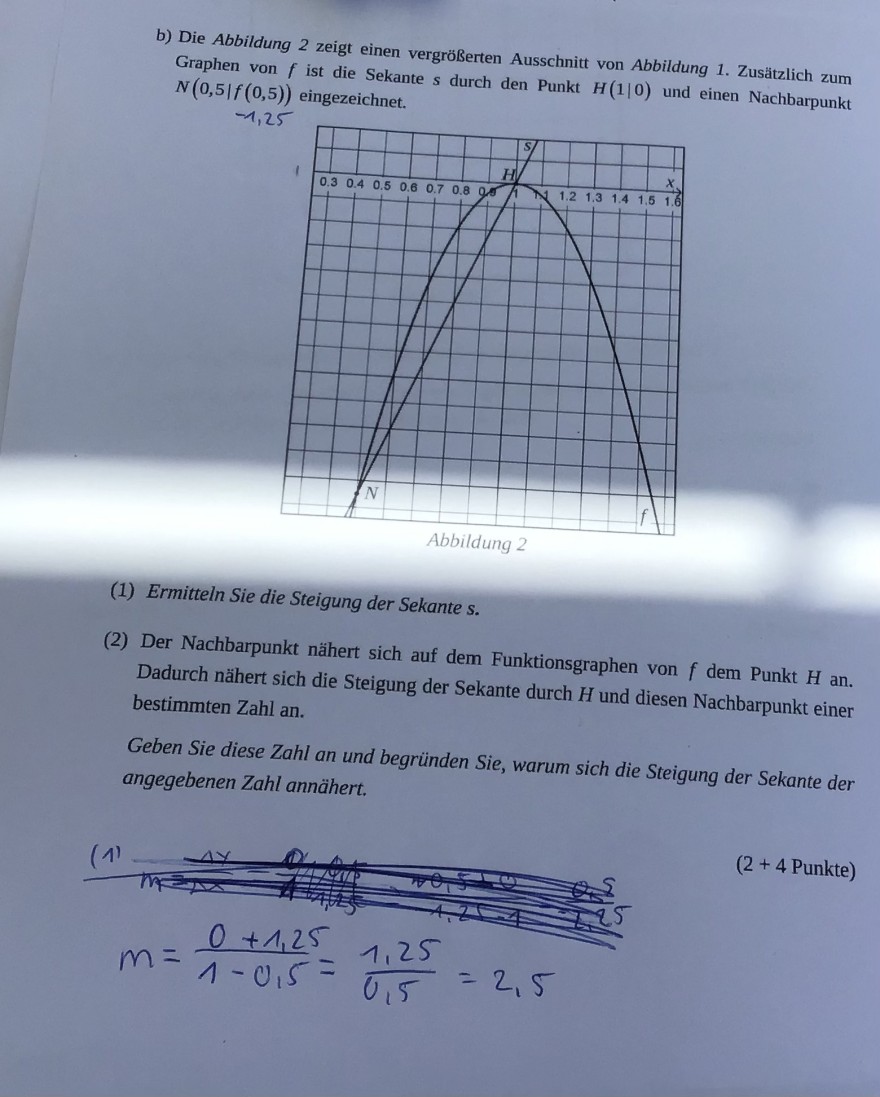

Text erkannt:

b) Die Abbildung 2 zeigt einen vergrößerten Ausschnitt von Abbildung 1. Zusätzlich zum Graphen von \( f \) ist die Sekante \( s \) durch den Punkt \( H(1 \mid 0) \) und einen Nachbarpunkt \( N(0,5 \mid f(0,5)) \) eingezeichnet.
Abbildung 2
(1) Ermitteln Sie die Steigung der Sekante s.
(2) Der Nachbarpunkt nähert sich auf dem Funktionsgraphen von \( f \) dem Punkt \( H \) an. Dadurch nähert sich die Steigung der Sekante durch \( H \) und diesen Nachbarpunkt einer bestimmten Zahl an.

Geben Sie diese Zahl an und begründen Sie, warum sich die Steigung der Sekante der angegebenen Zahl annähert.

Answer 1

(1)

m = (f(1) - f(0.5))/(1 - 0.5) = (0 - (-1.25))/0.5 = 2.5

(2)

Die Steigung nähert sich der Zahl null. weil die Tangente in einem Extrempunkt die Steigung Null hat.

Comments

Um eine Idee von (2) zu bekommen, könntest du mal m = (f(1) - f(0.999))/(1 - 0.999) berechnen.