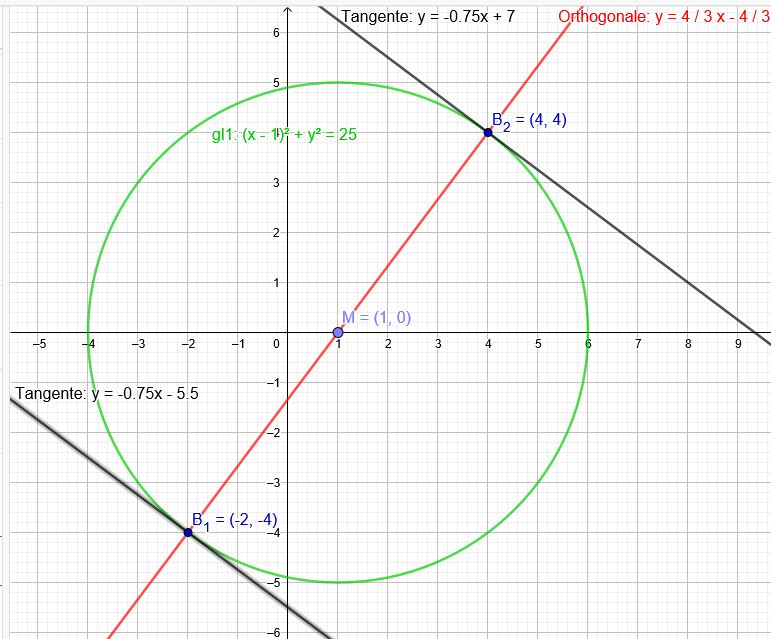
Ermittle in welchen Punkten des Kreises \(k:(x-1)^2 +y^2 = 25\) die jeweilige Tangente an den Kreis die Steigung \(-\frac{3}{4}\) hat?
Mittelpunkt des Kreises ist \(M(1|0)\)
Die Orthogonale durch M:
\( \frac{y-0}{x-1}= \frac{4}{3}\)
\( y= \frac{4}{3}*x- \frac{4}{3}\) schneidet den Kreis in:
\((x-1)^2 + (\frac{4}{3}*x- \frac{4}{3})^2 = 25\)
\(x_1=-2\) \(y_1=-4\)
\(x_2=4\) \(y_2=4\)