Welches Volumen hat der Dachstuhl und wie groß ist die Dachfläche?

Question

Aufgabe:

Ein Haus besitzt einen Dachstuhl, dessen Giebelseite ein gleichseitiges Dreieck bildet. Die Breite des Hauses an der Giebelseite misst \( b=9,12 \mathrm{~m} \), die Länge beträgt \( a=13,60 \mathrm{~m} \) und die Höhe des Hauses beträgt \( h=15,30 \mathrm{~m} \) (vgl. Skizze).

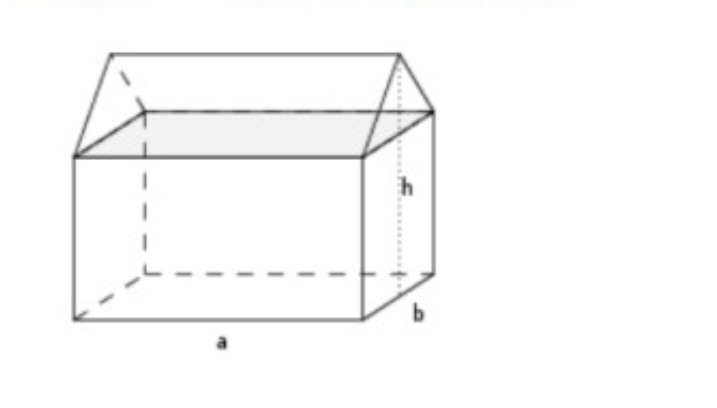
Welches Volumen hat der Dachstuhl und wie groß ist die Dachfläche (in \( \mathrm{m}^{3} \) bzw. \( \mathrm{m}^{2} \) )? Rechnen Sie mit den exakten Werten und runden Sie alle Ergebnisse auf zwei Nachkommastellen.

Problem/Ansatz:

Answer 1

Hallo,

stelle dir den Dachstuhl als Prisma mit dem gleichseitigen Dreieck als Grundfläche = G vor.

Das Volumen eines Prismas berechnest du mit \(V=G\cdot h\), die Höhe ist dann die Länge a und G der Flächeninhalt des Dreiecks.

Die Dachfläche sind zwei Rechecke mit den Seitenlängen a und b.

Gruß, Silvia

Comments

Die Dachfläche sind zwei Rechecke mit den Seitenlängen a und b.

Ich verstehe die Skizze vielmehr so, dass die Grundfläche ein Recheck mit den Seitenlängen a und b ist.

---

Ja, aber die Seitenlänge des Rechtecks ist doch genauso lang wie b, oder nicht?

---

Von den Dach-Rechtecken nicht, die sind ja schräg.

---

Giebel = gleichseitiges Dreieck, und die kürzere Seite des Rechtecks ist eine Seitenlänge des Dreiecks.

Was ist mein Denkfehler?

---

Herrjesses, da steht "gleichseitig". Sorry. Hat auf der Skizze so gar nicht gleichseitig ausgesehen.

Answer 2

Dachhöhe h über Pythagoras:

h^2= b^2-(b/2)^2 = 9,16^2- 4,56^2

h= 7,90 m

A(Dreieck) = b*h/2

V= A*a =

Answer 3

Silvia hat das ja schon perfekt erklärt. Hier nur noch eine Kontroll-Lösung.

a) V = 1/2·9.12·√(9.12^2 - (9.12/2)^2)·13.6 = 883728/3125·√3 = 489.81 m³

b) A = 2·9.12·13.6 = 31008/125 = 248.06 m²