Ungleichung einer mehrdimensionalen Funktion

Question

ich habe eine Frage zu einer Ungleichung einer mehrdimensionaler Funktion bei der ich mir sicher sein wollte, ob sie stimmt. Es ging darum, zu bestimmen, ob sie in (0,0) stetig ist, wobei (x,y)≠(0,0) gilt. Ich habe zuerst eine Ungleichung konstruiert, wobei xn und yn Folgen sind, die gegen den Ursprung konvergieren. Könnte jemand sie überprüfen ? Die Ungleichung befindet sich im Anhang.

Danke

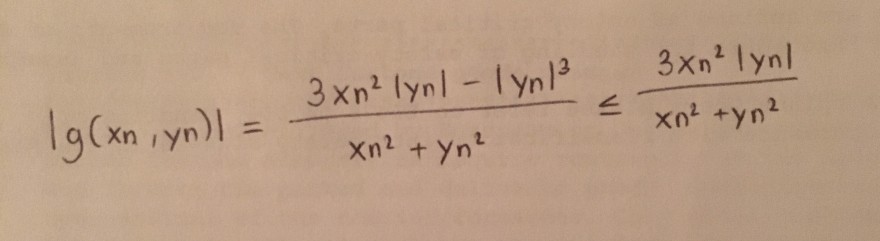
Text erkannt:

$|g(x n, y n)|=\frac{3 x n^{2}|y n|-|y n|^{3}}{x n^{2}+y n^{2}} \leq \frac{3 x n^{2}|y n|}{x n^{2}+y n^{2}}$

Comments

Die linke Gleichung kann so nicht stimmen, denn $|g(x_n,y_n)|\geq 0$, während $\frac{3x_n^2|y_n| - |y_n|^3}{x_n^2 + y_n^2}$ negativ werden kann, wenn $|x_n|$ klein gegen $|y_n|$ ist.

Beispiel: Setze $x_n = \frac 1{\sqrt 3 n^2}, y_n = \frac 1n$. Dann wird der Zähler negativ fur $n>1$.

---

Eigentlich sollte das „hoch 3“ im Zähler beim linken Quotienten im Betrag stehen, ich hatte mich nur verschrieben. Ist das der Fehler ?

---

Was ist denn der "linke Quotient"?

Es spielt übrigens keine Rolle hier, ob im Zähler $|y_n^3|$ oder $|y_n|^3$ steht.

Da $\frac{3x^2|y| - |y|^3}{x^2+y^2}$ negativ werden kann, kann es sich hier nicht um den Betrag irgendeiner Funktion handeln.

Also $\color{red}{|g(x,y)| = \frac{3x^2|y| - |y|^3}{x^2+y^2}} \text{muss falsch sein.}$

Ich vermute, du hast beim Bilden des Betrages deiner Funktion einen Fehler gemacht hast.

Schreib doch mal deine Funktion $g(x,y)$ hin.

---

Danke für die Antwort. Hier ist die Funktion g(x,y) 

Text erkannt:

$g(x, y)=\frac{3 x^{2} y-y^{3}}{x^{2}+y^{2}}$

---

Ich hab mal eine Antwort zu dieser Funktion geschrieben.

Answer 1

Aloha :)

Der Zähler ist klar, denn:$$|y_n|\ge0\implies|y_n|^3\ge0\implies-|y_n|^3\le0\implies3x_n^2|y_n|-|y_n|^3\le3x_n^2|y_n|$$Da der Nenner $x_n^2+y_n^2>0$ ist, bleibt das Relationszeichen bei der Division erhalten:$$\frac{3x_n^2|y_n|-|y_n|^3}{x_n^2+y_n^2}\le\frac{3x_n^2|y_n|}{x_n^2+y_n^2}\quad\checkmark$$

Comments

Vielen Dank!

---

Du hast die Ungleichung zwar korrekt gezeigt, aber mit der Fragestellung stimmt grundsätzlich etwas nicht, da links der Betrag einer Funktion steht und der abgeschätzte Term aber negativ werden kann.

---

Ja stimmt, das erste Gleichheitszeichen habe ich nicht überprüft.

Ich habe mich nur um das $\le$ gekümmert ;)

Answer 2

Du kannst deine Funktion wie folgt abschätzen:

$$\left|g(x,y)\right| = \left|\frac{3 x^{2} y-y^{3}}{x^{2}+y^{2}}\right| \leq |y| \left|\frac{3 x^{2} +y^{2}}{x^{2}+y^{2}}\right|$$

$$\leq |y| \left|\frac{3 x^{2} +3y^{2}}{x^{2}+y^{2}}\right| = 3|y| \stackrel{(x,y)\to (0,0)}{\longrightarrow} 0$$

Comments

Vielen Dank für die Mühe